Đáp án A
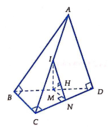
+ Gọi I là trung điểm AC (do Δ A B C vuông tại B)
⇒ I A = I C = I B = I D ⇒ I là tâm mặt cầu ngoại tiếp ABCD
+ Gọi M là trung điểm của BC => M là tâm đường tròn ngoại tiếp Δ B C D
⇒ I M là trục của đường tròn ngoại tiếp Δ B C D ⇒ I M ⊥ B C D
+ Gọi N, H lần lượt là hình chiếu của M lên CD và I N ⇒ M H ⊥ I C N
⇒ M H = d M ; I C N = d M ; A C D = 1 2 d B ; A C D = a 2 2
+ N là trung điểm của CD ⇒ M N = 1 2 B C = a 3 2
Có 1 I M 2 + 1 M N 2 = 1 M H 2 ⇒ I M 2 = 3 a 2 2
I C 2 = C M 2 + M H 2 = 3 a 2 ⇒ R = I C = a 3
⇒ V = 4 3 π R 3 = 4 3 π a 3 3 = 4 π a 3 3

