Gọi M là trung điểm của AB ta có:
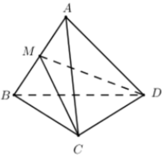
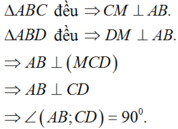
Chọn C.
Gọi M là trung điểm của AB ta có:

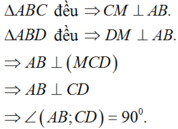
Chọn C.
Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Khoảng cách giữa hai đường thẳng AB và CD bằng 3 2 . Thể tích khối tứ diện ABCD bằng
A. 3 2
B. 1 2
C. 3 6
D. 1 6
Cho tứ diện ABCD có A B = A C = A D = 1 , B A C ^ = 60 ∘ , B A D ^ = 90 ∘ , D A C ^ = 120 ∘ Tính cosin của góc tạo bởi hai đường thẳng AG và CD, trong đó G là trọng tâm tam giác BCD.
A. 1 6
B. 1/3
C. 1/6
D. 1 3
Cho tứ diện ABCD có BC=a, C D = a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa hai đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
A. a 3 2
B. a 3
C. a
D. a 7 2
Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng 11 2 . Khi đó độ dài cạnh CD là
A. 2
B. 2
C. 1
D. 3
Cho tứ diện ABCD có tam giác ABD đều là cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng 11 2 . Khi đó độ dài cạnh CD là
A. 2
B. 1
C. 3
D. 2
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 ° . Tính thể tích V của khối tứ diện ABCD theo a:
A. V = a 3 8
B. V = a 3 3 16
C. V = a 3 2 8
D. V = a 3 2 12
Trong mặt phẳng (P) cho tam giác OAB cân tại O, O A = O B = 2 a , A O B ^ = 120 ° . Trên đường thẳng vuông góc với mặt phẳng (P) tại O lấy hai điểm C, D nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A. 3 a 2 2
B a 2 3
C. 5 a 2 2
D. 5 a 2 3
Trong mặt phẳng (P) cho tam giác OAB cân tại O , O A = O B = 2 a , A O B ^ = 120 ° . Trên đường thẳng vuông góc với măt phẳng (P) tại O lấy hai điểm C, D , nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A. 3 a 2 2
B. a 2 3
C. 5 a 2 2
D. 5 a 2 3
Cho khối tứ diện ABCD có B C = 3 , C D = 4 , A B C ^ = B C D ^ = A D C ^ = 90 ° Góc giữa hai đường thẳng AD và BC bằng 60 ° Côsin góc giữa hai mặt phẳng (ABC) và (ACD) bằng
A. 2 43 43
B. 43 86
C. 4 43 43
D. 43 43