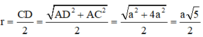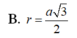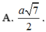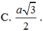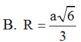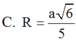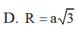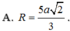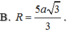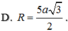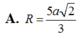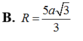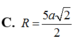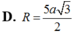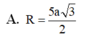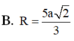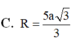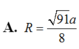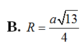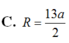Đáp án D
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
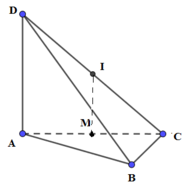
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu: