Đáp án A.
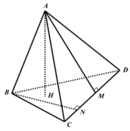
Gọi CD = a (0 < a ≤ 1); AM và BN lần lượt là đường cao của tam giác ACD và BCD; AH là chiều cao tứ diện ABCD.

Đáp án A.
Gọi CD = a (0 < a ≤ 1); AM và BN lần lượt là đường cao của tam giác ACD và BCD; AH là chiều cao tứ diện ABCD.


Cho khối tứ diện ABCD có A B = x , tất cả các cạnh còn lại bằng 2. Thể tích khối tứ diện đã cho đạt giá trị lớn nhất bằng
A. 1 2
B. 3 3 2
C. 2 2 3
D. 1
Cho tứ diện ABCD có độ dài cạnh Ab thay đổi và AB = x các cạnh còn lại bằng a không đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD là
A. 3 a 3 4
B. a 3 8
C. 3 a 3 8
D. a 3 4
Xét khối tứ diện ABCD có cạnh AD=x và các cạnh còn lại đều bằng a = 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất
A. x = 6
B. x = 14
C. x = 3 2
D. x = 2 3
Xét khối tứ diện ABCD có cạnh AD=x và các cạnh còn lại đều bằng 2. Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất.
A. x = 2 3
B. x = 6
C. x = 2
D. x = 3
Cho tứ diện ABCD có AB = x, tất cả các cạnh còn lại có độ dài bằng 2. Gọi S là diện tích tam giác ABC, h là khoảng cách từ D đến mp(ABC).Với giá trị nào của x thì biểu thức V = 1 3 S . h đạt giá trị lớn nhất.
A. x = 1
B. x = 6
C. x = 2 6
D. x = 2
Xét tứ diện ABCD có các cạnh A B = B C = C D = D A = 1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng.
A. 2 3 27
B. 4 3 27
C. 2 3 9
D. 4 3 9
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn: S A 2 + B C 2 = 18 và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng: V m a x = x y 4 ; x , y ∈ ℕ * ; x , y = 1. Khi đó: x, y thỏa mãn bất đẳng thức nào dưới đây?
A. x + y 2 − x y > 4550.
B. x y + 2 x y > 2550.
C. x 2 − x y + y 2 < 5240.
D. x 3 − y > 19602.
Xét khối tứ diện ABCD,AB= x, các cạnh còn lại bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD lớn nhất
A. x = 6
B. x = 2 2
C. x = 14
D. x = 3 2
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi V 1 ; V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2
A. 17 2 216
B. 17 2 72
C. 17 2 144
D. 2 12