Cho tứ diện ABCD có A D ⊥ ( A B C ) , đáy ABC thỏa mãn điều kiện c o t A + c o t B + c o t C 2 = B C A B . A C + C A B C . B A + A B C A . C B . Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC. Tính thể tích V của khối cầu ngoại tiếp khối chóp A.BCHK
A. V = 32 π 3
B. V = 8 π 3
C. V = 4 π 3 3
D. V = 4 π 3
Đáp án A
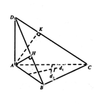
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Do tam giác AHB vuông tại H nên I thuộc trục của tam giác AHB. Tương tự I cũng thuộc trục của tam giác AKC. Suy ra I cách đều A, B, H,K, C nên nó là tâm mặt cầu ngoại tiếp hình chóp A.BCKH.
Gọi R là bán kính mặt cầu ngoại tiếp hình chóp A.BCKH thì R cũng là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có:
cot A + cot B + cot C = b 2 + c 2 - a 2 4 S + a 2 + c 2 - b 2 4 S + a 2 + b 2 - c 2 4 S = a 2 + b 2 + c 2 4 S
Nên c o t A + c o t B + c o t C 2 = B C A B . A C + C A B C . B A + A B C A . C B
⇔ a 2 + b 2 + c 2 8 S = a . sin A b c . sin A + b . sin B c a . sin B + c . sin C a b . sin C
⇔ a 2 + b 2 + c 2 8 S = a 2 4 R S + b 2 4 R S + c 2 4 R S ⇔ R = 2 ⇒ V = 4 3 πR 3 = 32 π 3


