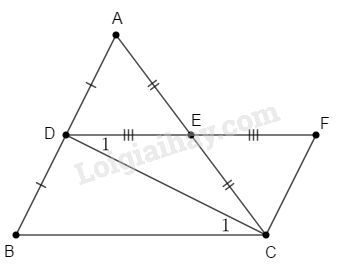
a) Xét 2 \(\Delta\) \(ADE\) và \(CFE\) có:
\(AE=CE\) (vì E là trung điểm của \(AC\))
\(\widehat{AED}=\widehat{CEF}\) (vì 2 góc đối đỉnh)
\(DE=FE\) (vì E là trung điểm của \(DF\))
=> \(\Delta ADE=\Delta CFE\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta ADE=\Delta CFE.\)
=> \(AD=CF\) (2 cạnh tương ứng).
Mà \(AD=DB\) (vì D là trung điểm của \(AB\))
=> \(DB=CF.\)
c) Theo câu a) ta có \(\Delta ADE=\Delta CFE.\)
=> \(\widehat{ADE}=\widehat{CFE}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AD\) // \(CF.\)
Hay \(AB\) // \(CF.\)
d) Vì \(AB\) // \(CF\left(cmt\right)\)
=> \(BD\) // \(CF.\)
=> \(\widehat{BDC}=\widehat{FCD}\) (vì 2 góc so le trong).
Xét 2 \(\Delta\) \(DBC\) và \(CFD\) có:
\(DB=CF\left(cmt\right)\)
\(\widehat{BDC}=\widehat{FCD}\left(cmt\right)\)
Cạnh DC chung
=> \(\Delta DBC=\Delta CFD\left(c-g-c\right)\)
=> \(\widehat{DCB}=\widehat{CDF}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(DF\) // \(BC.\)
Hay \(DE\) // \(BC\left(đpcm\right).\)
Chúc bạn học tốt!
a và b)
Xét \(ΔAED\) và \(ΔCEF\) có:
\(AE=CE\)(vì $E$ là trung điểm của $AC$)
\(\widehat{AED}=\widehat{CEF}\)(đối đỉnh)
$ED=EF$(vì $E$ là trung điểm của $DF$)
nên: $ΔAED=ΔCEF$(c-g-c)
do đó: $AD=CF$
mà $AD=BD$ (vì $D$ là trung điểm của $AB$)
vậy $BD=CF$
c) Ta có: \(\widehat{EAD}=\widehat{ECF}\)(vì $ΔAED=ΔCEF$)
mà hai góc này ở vị trí so le trong
nên $AB//CF$
d) Ta có:$AB//CF(cmt)$
nên \(\widehat{BDC}=\widehat{FCD}\) (hai góc so le trong)
Xét: $ΔBDC$ và $ΔFCD$ có:
$DC$ là cạnh chung
\(\widehat{BDC}=\widehat{FCD}\) (cmt)
$DB=CF(cmt)$
nên $ΔBDC=ΔFCD(c-g-c)$
Ta có: \(\widehat{BCD}=\widehat{FDC}\)(vì $ΔBDC=ΔFCD$)(mà hai góc này ở vị trí so le trong) nên $DE//BC$


