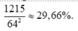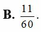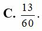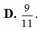Chọn B
Số tập con của S là 2 6 = 64
Mỗi người có 64 cách chọn tập con, do vậy số phần tử của không gian mẫu là: 64 2
Ta tìm số cách chọn tập con thỏa mãn yêu cầu:
Giả sử tập con của A và B chọn được lần lượt có x,y phần tử ![]()
Khi đó: A có C 6 x cách chọn tập con, lúc này S còn 6 - x phần tử.
Ta chọn ra 2 phần tử gọi là a,b từ x phần tử trong tập con của A để xuất hiện trong tập con của B, có C x 2 cách.
Như vậy, tập con của B đã có 2 phần tử chung với tập con của A là a,b ta cần chọn thêm (y-2) phần tử khác trong (6-x) phần tử còn lại sau khi A đã chọn tập con,ở bước này có C 6 - x y - 2 cách chọn.
Vậy có: C 6 x C 6 - x y - 2 cách chọn tập con thỏa mãn.
Ta có điều kiện:
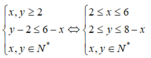
Cho x nhận các giá trị từ 2 đến 6, số cách chọn tập con thỏa mãn yêu cầu đề bài là:
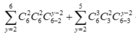
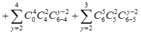
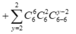
= 240 + 480 + 360 + 120 + 15 = 1215
Xác suất cần tính bằng: