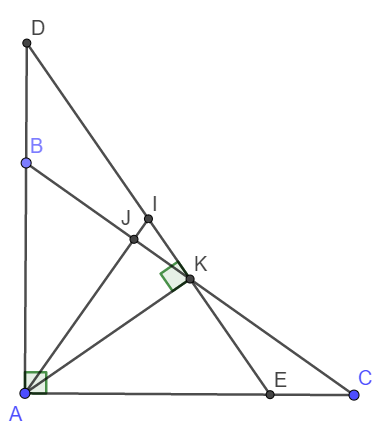
a) Xét tam giác vuông ABC có K là trung điểm nên theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: KB = KA
Hay tam giác KAB cân tại K, suy ra \(\widehat{KBA}=\widehat{KAB}\)
Xét tam giác vuông ADE có I là trung điểm nên theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: ID = IA
Hay tam giác IDA cân tại I, suy ra \(\widehat{IAB}=\widehat{IDA}\)
Vậy nên ta có: \(\widehat{KBA}+\widehat{IAB}=\widehat{KAB}+\widehat{IDA}=90^o\left(\widehat{DKA}=90^o\right)\)
Gọi giao điểm của BC và AI là J.
Xét tam giác ABJ có \(\widehat{JBA}+\widehat{JAB}=90^o\Rightarrow\widehat{BJA}=90^o\)
Vậy nên \(AI\perp BC.\)
b) Ta thấy ngay \(DE=2AI;BC=2AK\)
Mà theo quan hệ giữa đường vuông góc và đường xiên thì \(AI\ge AK\)
Vậy nên \(DE\ge BC\).
Bạn xuất sắc lắm Lê Xuân Huy
