Cho tam giác nhọn ABC nội tiếp đường tròn (O). M, N là hai điểm thuộc cung nhỏ A C ⏜
sao cho MN song song với AC và tia BM nằm giữa hai tia BA, BN. BM giao AC tại P.
Gọi Q là một điểm thuộc cung nhỏ B C ⏜ sao cho PQ vuông góc với BC. QN giao AC tại R
3) Gọi F là giao của AQ và BN. Chứng minh rằng A F B ^ = B P Q ^ + A B R ^ .
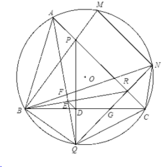
Ta có:
B P Q ^ = B R Q ^ = R B N ^ + R N B ^ = E B F ^ + B A E ^ = 90 0 − B F E ^ + 90 0 − A B E ^ = 180 0 − B F E ^ − A B E ^ = A F B ^ − A B R ^ ⇒ A F B ^ = B P Q ^ + A B R ^

