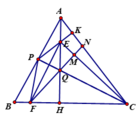
Trong tam giác EFC có C Q ⊥ E F (do EF là trung trực PQ); E Q ⊥ F C nên F Q ⊥ E C .
Từ đó
E
M
N
^
=
90
0
, nên tứ giác EKNM nội tiếp đường tròn đường tròn đường kính ![]() .
.
Ta có tứ giác EKCH nội tiếp đường tròn đường kính EC nên P E Q ^ = H C K ^ .
Chú ý: EF là phân giác góc PEQ và CQ là phân giác góc HCK, do đó P E F ^ = 1 2 P E Q ^ = 1 2 H C K ^ = P C F ^ . Do đó tứ giác PECF nội tiếp.

