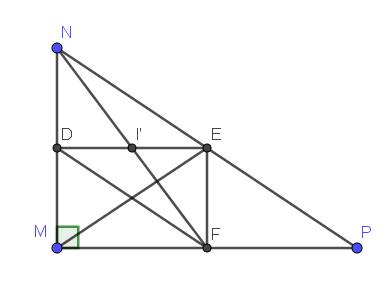
Lời giải:
a. $D,E,F$ là trung điểm $MN,NP,MP$ nên $EF, DE$ lần lượt là đường trung bình của tam giác $ABC$ ứng với lần lượt 2 cạnh $MN, MP$
$\Rightarrow EF\parallel MN, DE\parallel MP$
Mà $MN\perp MP$ nên $EF\perp MP, DE\perp MN$
$\Rightarrow \widehat{EFM}=\widehat{EDM}=90^0$
Tứ giác $MDEF$ có 3 góc vuông $\widehat{M}=\widehat{D}=\widehat{F}$ nên là hình chữ nhật.
b.
Gọi $I'$ là giao điểm $NF$ và $DE$
Do $DE\parallel MP$ nên $DI'\parallel MF$
Áp dụng định lý Talet:
$\frac{DI'}{MF}=\frac{ND}{NM}=\frac{1}{2}$
$\Rightarrow MF=2DI'$
Mà $MF=DE$ (do $MFED$ là hcn)
$\Rightarrow DE=2DI'$
$\Rightarrow I'$ là trung điểm của $DE$
$\Rightarrow I\equiv I'$
Mà $I', N, F$ thẳng hàng nên $I, N, F$ thẳng hàng.
c.
Có: $\frac{NI}{NF}=\frac{ND}{NM}=\frac{1}{2}$ nên $I$ là trung điểm $NF$
$DF$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow DF=\frac{1}{2}NP\Rightarrow ME=DF=\frac{1}{2}NP$.
Khi đó ta có:
$NF.ME-IF.PE = 2IF.\frac{1}{2}NP-IF.PE$
$=IF.NP-IF.PE = IF(NP-PE) = IF.NE$