Các câu hỏi tương tự
Cho tam giác ABC đồng dạng với tam giác A’B’C’ tỉ số đồng dạng là 1/2 biết AB=3cm AC=4cm BC=5cm
a) tính các cạnh của tam giác A’B’C’
b) vẽ MN song song với B’C’ . Chứng minh tam giác ABC đồng dạng với tam giác A’MN
c) Biết A’M=4cm. Tính A’M; MN
d) kẻ A’H vuông góc với B’C’; A’H cắt MN tại K. Tính A’H và A’K
Cho tam giác ABC có góc A=90 độ; AB=3cm; AC=4cm và tam giác MNP có N=90 độ; MN=8cm; MP=10cm
a) Tính BC và NP
b) Chứng minh tam giác ABC đồng dạng với tam giác NPM
Cho tam giác ABC có góc A=90 độ; AB=3cm; AC=4cm và tam giác MNP có N=90 độ; MN=8cm; MP=10cm
a) Tính BC và NP
b) Chứng minh tam giác ABC đồng dạng với tam giác NPM
Cho tam giác ABC có góc A=90 độ; AB=3cm; AC=4cm và tam giác MNP có N=90 độ; MN=8cm; MP=10cm
a) Tính BC và NP
b) Chứng minh tam giác ABC đồng dạng với tam giác NPM
Tính diện tích của hình được cho trong mỗi trường hợp sau đây: Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs. 25)
Biết AB = 13cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD
Cho tam giác ABC, I là giao điểm các đường phân giác trong của tam giác đó, từ I kẻ IM vuông góc vs AB, IN vuông góc vs BC, IK vuông góc vs AC. Qua A vẽ D1 // MN cắt NK ở E. Qua A vẽ D2// NK cắt MN tại D. Đường thẳng ED cắt AC ở P, cắt AB ở Q
Chứng minh PQ là đường trung bình của t/giác ABC
Cho tam giác ABC có AB = 3cm; AC = 4cm và BC = 5cm. Tam giác MNP vuông tại M có MN = 6cm; MP = 8cm. Tìm khẳng định sai
A. Tam giác ABC là tam giác vuông
B. Δ ABC và ΔMNP đồng dạng với nhau
C. NP = 10 cm
D. Có hai phương án sai
Cho tam giác ABC có cạnh BC = 8cm và có D, E, M, N lần lượt là trung điểm của AB,AC,BD và EC (như hình vẽ). Khi đó MN = ?
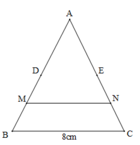
A. 7cm
B. 5cm
C. 6cm
D. 4cm
Cho tam giác ABC . Gọi I là giao điểm của các tia phân giác trong . Kẻ IM vuông góc với AB ; IN vuông với BC; IK vuông với AC . Qua A vẽ đường thẳng a//MN ; b//NK . a giao NK tại E ; b giao MN tại D . ED lần lượt giao AC;AB tại P:Q . CMR : PQ // BC



