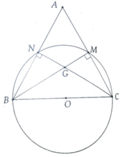
a, Ta có: B N C ^ = 90 0 => N ∈ (O; B C 2 )
B M C ^ = 90 0 => M ∈ (O; B C 2 )
=> B, C, M, N cùng thuộc đường tròn tâm (O; B C 2 )
b, ∆ABC đều có G là trực tâm đồng thời là trọng tâm
∆AOB vuông tại O có R = ON = a 2
Ta có OA = a 2 - a 2 4 = a 3 2 > R
=> A nằm ngoài (O)
Ta có OG = 1 3 OA = a 3 6 < R
=> G nằm ngoài (O)

