hình như cj ms hỏi là AD nó sao á em=)?
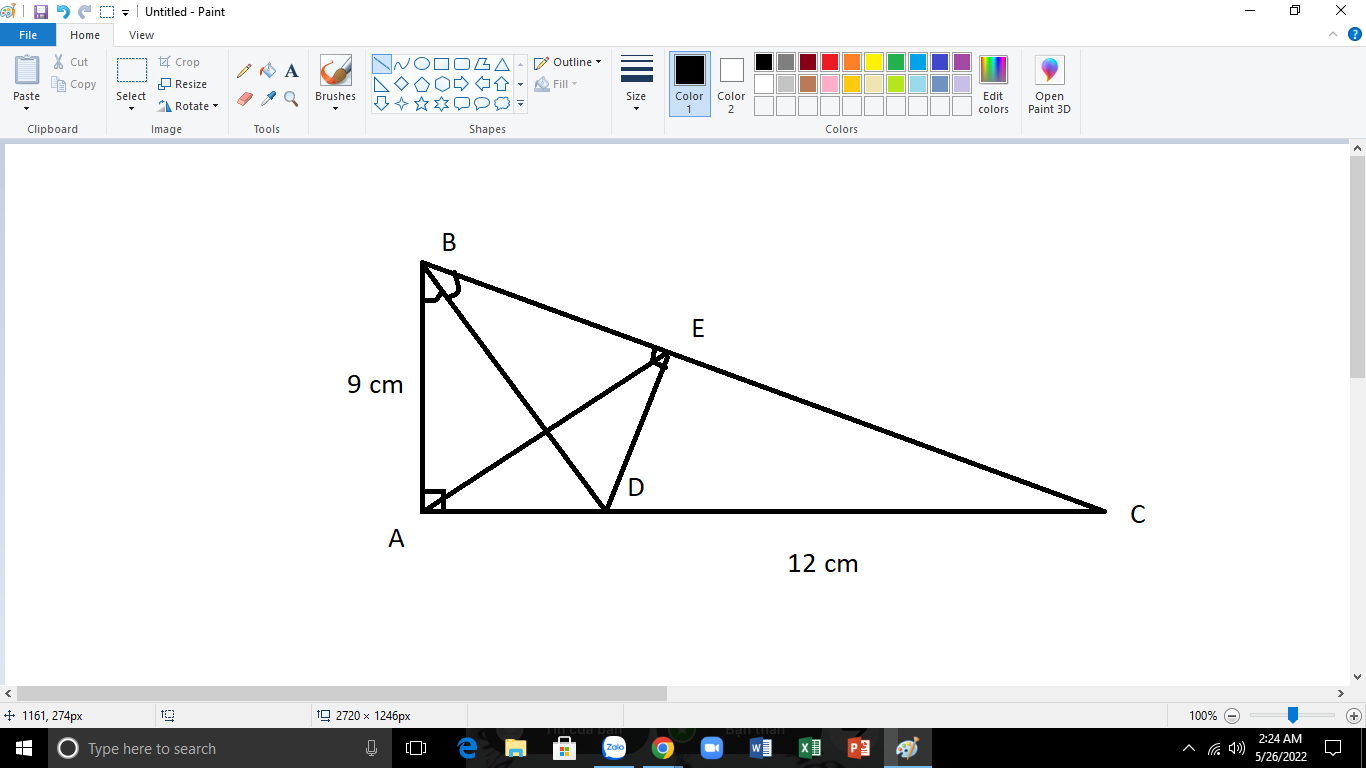
\(\text{a)Xét }\Delta ABC\text{ vuông tại A có:}\)
\(BC^2=AB^2+AC^2\left(\text{định lí Py ta go}\right)\)
\(\Rightarrow BC^2=9^2+12^2=81+144=225\left(cm\right)\)
\(\Rightarrow BC=\sqrt{225}=15\left(cm\right)\)
\(\text{b)Xét }\Delta ABD\text{ và }\Delta EBD\text{ có:}\)
\(\left\{{}\begin{matrix}\widehat{ABD}=\widehat{EBD}\left(BD\text{ là phân giác }\widehat{B}\right)\\BD\text{ chung}\\\widehat{BAD}=\widehat{BED}=90^0\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABD=\Delta EBD\left(ch-gn\right)\)
\(\text{c)Vì }\Delta ABD=\Delta EBD\left(cmt\right)\)
\(\Rightarrow AD=DE\left(\text{hai cạnh tương ứng}\right)\)
\(\text{d)Ta có:AB=EB}\left(\Delta ABD=\Delta EBD\right)\)
\(\Rightarrow\Delta ABE\text{ cân tại B}\)
\(\text{e)Xét }\Delta DEC\text{ vuông tại E có:}\)
\(DC\text{ là cạnh huyền lớn nhất}\)
\(\Rightarrow DC>DE\left(1\right)\)
\(\text{Ta có:AD=DE(cmt)(2)}\)
\(\text{Từ (1) và (2)}\)
\(\Rightarrow AD< DC\)




