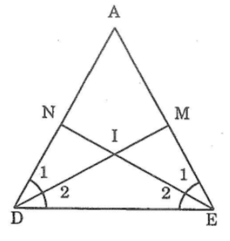
Tam giác ADE có: ∠D = ∠E (giả thiết) (1)
∠(D1) = ∠(D2) = (1/2)∠D (vì DM là tia phân giác của góc ADE) (2)
∠(E1) = ∠(E2) = (1/2)∠E (vì EN là tia phân giác của góc AED) (3)
Từ (1); (2) và (3) suy ra: ∠(D1 ) = ∠(D2) = ∠(E1) = ∠(E2 )
+) Xét ΔDNE và ΔEMD, ta có:
∠(NDE) = ∠(MED) (giả thiết)
DE cạnh chung
∠(D2) = ∠(E2 ) (chứng minh trên)
Suy ra: ΔDNE = ΔEMD (g.c.g)
Vậy DN = EM (hai cạnh tương ứng)

