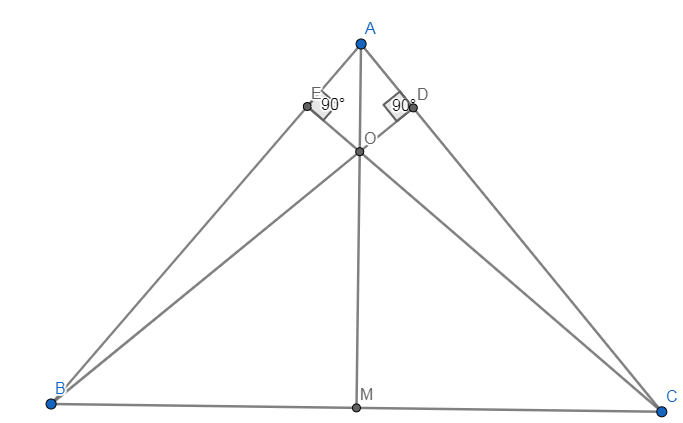
\(a,Xét\) \(\Delta ABD\) \(và\) \(\Delta ACE\) \(có\):
\(\widehat{A}\) \(chung\)
\(AB=AC\) (\(\Delta ABC\) \(cân\) \(tại A)\)
\(\widehat{ACE}=\widehat{ADE}\) \((cùng\) \( phụ\) \( với\) \(\text{ 2 góc còn lại)}\)
\(\Rightarrow\Delta ABD=\Delta ACE\left(g.c.g\right)\)
\(\Rightarrow BD=CE\) \(\text{(cạnh tương ứng)}\)
\(\left(đpcm\right)\)
\(b,\) \(Ta\) \(thấy\) \(AE=AD\) (\(Do\) \(\Delta ABD=\Delta ACE\))
\(Xét\) \(\Delta AEO\) \(và\) \(\Delta ADO\) \(có:\)
\(AE=AD\)
\(AO\) \(chung\)
\(\Rightarrow\Delta AEO=\Delta ADO\left(c.h;c.g.v\right)\)
\(\widehat{EAO}=\widehat{DAO}\) (\(góc\) \(tương\) \(ứng\))
\(\Rightarrow AO\) \(là\) \(phân\) \(giác\) \(góc\) \(\widehat{BAC}\)
\(c,\) Nối A với M, Xét \(\Delta AMB\) và \(\Delta AMC\) có:
\(AB=AC\)
\(AM\) chung
\(BM=MC\)
\(\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\Rightarrow\widehat{BAM}=\widehat{CAM}\) (góc tương ứng)
\(\Rightarrow AM\) là phân giác góc \(\widehat{BAC}\)
Mà AO cũng là phân giác góc \(\widehat{BAC}\)
\(\Rightarrow A,O,M\) thẳng hàng
\(\left(đpcm\right)\)

