Các câu hỏi tương tự
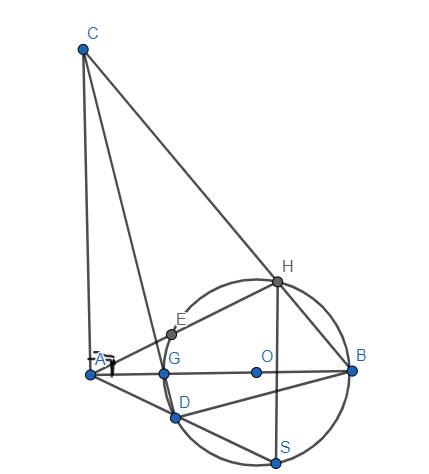
cho tam giác ABC vuông tại A vẽ đtròng (GB) cắt BC tại H ,AH cắt đtrong tại E BG cắt dtròn tại D ,AD cắt đtròn tại S
a)BA là tia pg CBS
b) HS//AB
*giúp mk câu b vs
Cho tam giác vuông ABC có cạnh AC>AB đường cao AH(H thuộc BC). Trên tia HC lấy điểm D sao cho HD=HA. Đường vuông góc với BC tại D cắt AC tại E
a, CM: hai tam giác BEC và ADC đồng dạng
b, CM: Tam giác ABE cân
c,Gọi M là trung điểm của BE và vẽ tia AM cắt BG tại G. CMR:\(\frac{GB}{BC}=\frac{HD}{AH+HC}\)
Cho tam giác vuông ABC có cạnh AC>AB đường cao AH(H thuộc BC). Trên tia HC lấy điểm D sao cho HD=HA. Đường vuông góc với BC tại D cắt AC tại E
a, CM: hai tam giác BEC và ADC đồng dạng
b, CM: Tam giác ABE cân
c,Gọi M là trung điểm của BE và vẽ tia AM cắt BG tại G. CMR:\(\frac{GB}{BC}=\frac{HD}{AH+HC}\)
Cho tam giác ABC vuông tại A.Vẽ đtròn tâm o đường kính AB cắt BC tại điểm H .KẺ OK vuông góc với AH tại K và tia OK cắt AC tại D
a) Cm Dh là t tuyến của đtròn o
b) từ tđ I của Ak kẻ Đthằng vuông góc với AB và cắt đường tròn tại điểm M .Cm AK=AM
Cho tam giác ABC vuông tại A (ABAC). Vẽ đường tròn tâm O đường kính AB cắt BC tại H.a) Chứng minh AH vuông góc BCb) Gọi I là trung điểm AB. Chứng minh IH là tiếp tuyến (O)c) Tia phân giác góc HAC cắt BC tại E, cắt (O) tại D. Chứng minh AD * DE DC2d) Cho AB 12, AC 16. Tính bán kính đường tròn nội tiếp tam giác IAHGIẢI GIÚP EM CÂU D THÔI Ạ GIÚP EM GẤP
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC). Vẽ đường tròn tâm O đường kính AB cắt BC tại H.
a) Chứng minh AH vuông góc BC
b) Gọi I là trung điểm AB. Chứng minh IH là tiếp tuyến (O)
c) Tia phân giác góc HAC cắt BC tại E, cắt (O) tại D. Chứng minh AD * DE = DC2
d) Cho AB = 12, AC = 16. Tính bán kính đường tròn nội tiếp tam giác IAH
GIẢI GIÚP EM CÂU D THÔI Ạ GIÚP EM GẤP
1, Cho tam giác nhọn ABC co H là trực tâm, gọi M,N lần lượt là trung điểm của BC và AH. Đường phân giác trong góc A cắt MN tại K. CM AK vuông góc vs HK
2, Cho tam giác ABC nội tiếp đường tròn (O), Gọi AH, AD lần lượt là đường cao, đường phan giác trong của tam giác ABC (H,D thuộc BC). Tia AD cắt (O) tại E, tia EH cắt (O) tại F vaf tia FD cắt (O) tại K. CM AK là đường kính của (O)
tam giác abc có a = 90 độ ( ab<ac ) . Vẽ ( o ) đường kính ac cắt bc tại h a) ah vuông góc bc b) gọi m là trung điểm ab . C/m hm là tiếp tuyến của ( O ) c) tia phân giác của góc hac cắt bc tại e và cắt ( O ) tại d . C/m DA.DE = DC ²
Xem chi tiết
TV
28 tháng 3 2023 lúc 20:38
Cho tam giác ABC nhọn ( AB < AC ) nội tiếp ( O ). Tiếp tuyến tại A cắt BC tại S. I là trung điểm của BC. Tia OI cắt ( O ) tại D. Vẽ đường kính DF của (O). SF cắt (O) tại M. Kẻ AH vuông góc với SO, AH cắt BC tại N. Chứng minh : M, N, D thẳng hàng.
TV
29 tháng 3 2023 lúc 21:36
Cho tam giác ABC nhọn ( AB < AC ) nội tiếp ( O ). Tiếp tuyến tại A cắt BC tại S. I là trung điểm của BC. Tia OI cắt ( O ) tại D. AD cắt BC tại E. Vẽ đường kính DF của (O). SF cắt (O) tại M. CM : SE là tiếp tuyến của đường tròn ngoại tiếp tam giác MEF.