Bài 4:Cho tam giác abc vuông tại A.Từ C kẻ Cx vuông góc với BC,gọi F là giao điểm của Cx và phân giác góc ABC,BF cắt AC tại E.Kẻ CD vuông góc với EF tại D,kéo dài BA cắt CD tại Sa)Chứng minh CD là phân giác góc ECFb)DEDF và SE//CFFBài 5:Cho tam giác ABC cân tại A,góc A nhọn,đường phân giác AD.Trên tia đối tia DC lấy điểm M sao cho MDADDa)Chứng minh tam giác ADM vuông cânb)Kẻ BN vuông góc AM tại N,BN cắt AD tại O,chứng minh OM vuông góc ABBc)Chứng minh...
Đọc tiếp
Bài 4:Cho tam giác abc vuông tại A.Từ C kẻ Cx vuông góc với BC,gọi F là giao điểm của Cx và phân giác góc ABC,BF cắt AC tại E.Kẻ CD vuông góc với EF tại D,kéo dài BA cắt CD tại S
a)Chứng minh CD là phân giác góc ECF
b)DE=DF và SE//CFF
Bài 5:Cho tam giác ABC cân tại A,góc A nhọn,đường phân giác AD.Trên tia đối tia DC lấy điểm M sao cho MD=ADD
a)Chứng minh tam giác ADM vuông cân
b)Kẻ BN vuông góc AM tại N,BN cắt AD tại O,chứng minh OM vuông góc ABB
c)Chứng minh OB=OC; AM//OC
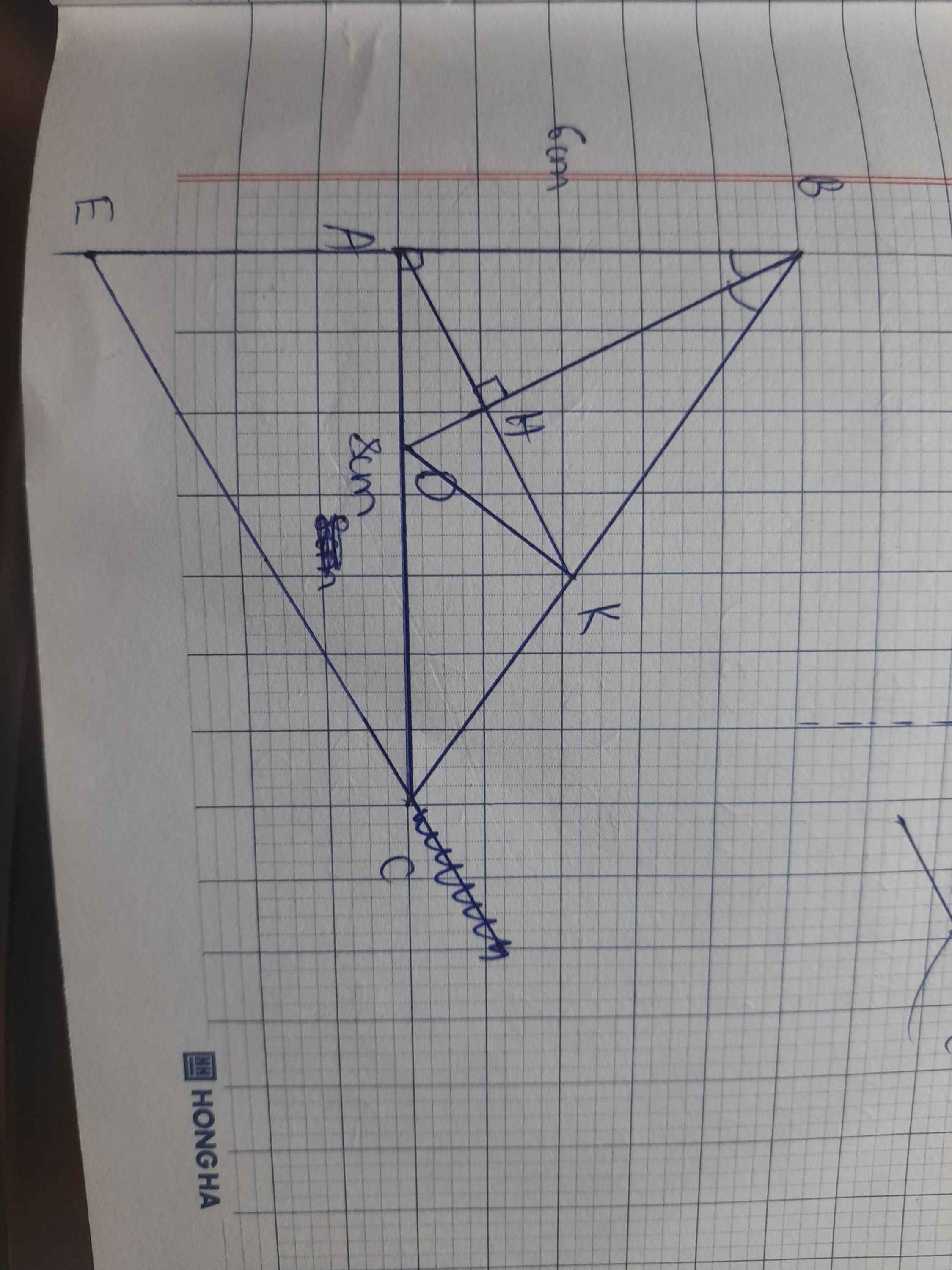
Bài 6:Cho tam giác ABC vuông tại A(AB<AC),đường cao AHH,trên cạnh BC lấy điểm M sao cho BA=BMM
a)Chứng minh AM là phân giác của góc HAC
b)Gọi K là hình chiếu vuông góc của M trên AC,chứng minh AM là đường trung trực HK
c)I là hình chiếu vuông góc của C trên AM,chứng minh AH,KM,CI cùng đi qua 1 điểm
Vẽ hình luôn giúp mình