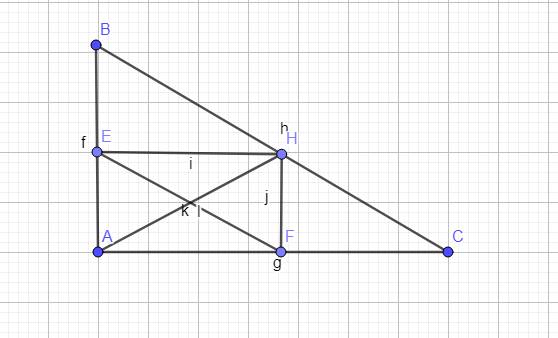
Ta có: tam giác vuông EBH \(\sim\) tam giác vuông ABC (gt)
=>\(\dfrac{S\Delta EBH}{S\Delta ABC}=\left(\dfrac{BH}{BC}\right)^2\Rightarrow\dfrac{\sqrt{S\Delta EBH}}{\sqrt{S\Delta ABC}}=\dfrac{BH}{BC}\left(1\right)\)
Ta có tam giác vuông FHC \(\sim\) tam giác vuông ABC (g.g)
=>\(\dfrac{S\Delta FHC}{S\Delta ABC}=\left(\dfrac{HC}{BC}\right)^2\Rightarrow\dfrac{\sqrt{S\Delta FHC}}{\sqrt{S\Delta ABC}}=\dfrac{HC}{BC}\left(2\right)\)
\(\)Từ (1)và (2) =>\(\dfrac{\sqrt{S\Delta EBH}+\sqrt{S\Delta FHC}}{\sqrt{S\Delta ABC}}=\dfrac{HB+HC}{BC}=\dfrac{BC}{BC}=1\)
Vậy \(\sqrt{S\Delta_{EBH}}+\sqrt{S\Delta_{FHC}}=\sqrt{S\Delta_{ABC}}\left(đpcm\right)\)
chucbanhoctot!
thực ra ở đây ko thể c/m đc yêu cầu của bạn đâu, cần phải có AEHF là hcn mới ra cơ ạ

