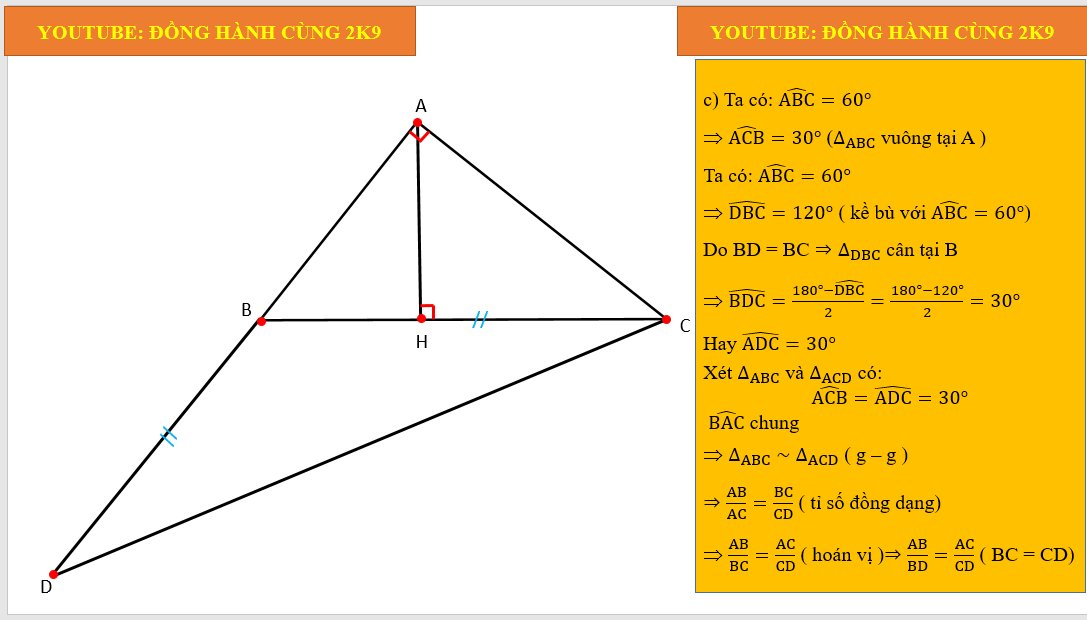
a: AB=BC*cos60=6*1/2=3cm
AC=căn 6^2-3^2=3*căn 3\(\simeq5.2\left(cm\right)\)
b: HB=AB^2/BC=1,5cm
HC=6-1,5=4,5cm
c) Tam giác BCD, có: BC=BD=> Tam giác BCD cân tại B=>BDC=BCD
Mặt khác: BDC+BCD=ABC=60 độ (tính chất góc ngoài của tam giác)
=>BDC=BCD=30 độ
Tam giác ABC vuông tại A, có: ABC+ACB=90 độ
=>ACB=90 độ-ABC=90 độ-60 độ=30 độ
=>ACD= DCB+BCA=30 độ+30 độ= 60 độ
Xét 2 tam giác ABC và ACD,có:
ABC=ACD=60 độ
ACB=ADC=30 độ
=> tam giác ABC đồng dạng tam giác ACD (g-g)
=>\(\dfrac{AB}{BC}=\dfrac{AC}{CD}\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\) (vì BD=BC)