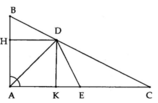

c) Do DH vuông góc với AB nên DH là khoảng cách từ D đến AB.
Tương tự DK là khoảng cách từ D đến AC.
Suy ra DH = DK. Suy ra điểm D cách đều AB và AC.


c) Do DH vuông góc với AB nên DH là khoảng cách từ D đến AB.
Tương tự DK là khoảng cách từ D đến AC.
Suy ra DH = DK. Suy ra điểm D cách đều AB và AC.
Cho tam giác ABC vuông tại A; AC = 2AB. Gọi E là trung điểm của AC, tia phân giác của
góc A cắt BC tại D.
a) Chứng minh: ∆BAD = ∆EAD
b) Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh điểm D cách đều AB và AC.
cho tam giác ABC vuông tại A có AB = 3cm,AC=6cm.Gọi E là trung điểm AC,tia phân giác của góc A cắt BC tại D
a) tính BD
b) chứng minh: tam giác BAD = tam giác EAD
c)Gọi H,K lần lượt là hình chiếu của D trên AB,AC.Chứng minh điểm D cách đều AB và AC
Bài 2. Cho ABC có A = 120°. Tia phân giác của A cắt BC tại D. Tia phân giác của
ADC cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB,
BC, AD. Chứng minh:
a) AC là tia phân giác của DAH .
b) IH = IK
Bài 5. Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH
AC (HAC). Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng
minh:
a) Chứng minh AB //HK
b) Chứng minh KAH IAH
c) Chứng minh AKI cân
Bài 7. Cho ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao
cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE = CD b) BMD = CME
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh
MN / / AC //BD.
Bài 8. Cho xOy . Lấy các điểm A,B thuộc tia Ox sao cho OA > OB. Lấy các điểm C, D
thuộc Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC
Chứng minh.:
a) AD = BC b) ABE = CDE
c) OE là tia phân giác của góc xOy
Bài 1: Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA. Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D.
a) Tính độ dìa AC khi AB= 9cm, BC= 15cm
b) Chứng minh: Tam giác ABD=tam giác EBD
c) Gọi H là giao điểm của đường thẳng AB và đường thẳng d. Chứng minh tam giác HBC cân
d) Chứng minh: AD<DC
Bài 2: Cho tam giác ABC vuông tại A có AB= 12cm, AC= 16cm.Kẻ BF là đường trung tuyến của tam giác ABC. Từ điểm C kẻ đường thẳng vuông góc với AC cắt đường trung tuyến BF tại D
a) Tính độ dài BC?
b) Chứng minh rằng: Tam giác ABF=tam giác CDF
c) Chứng minh: BF<(AB+BC):2
Bài 3: Cho tam giacsABC vuông tại A; tia phân giác của góc B cắt AC tại D. Kẻ DH vuông góc với BC\(\left(H\in BC\right)\). Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 9cm, AC= 12cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh: Tam giác KDC cân
d) Chứng minh: AB+AC>BD+DC
Bài 4: Cho tam giác ABC vuông tại A. Trên tia BC lấy điểm H sao cho BH=BA. Tia phân giác của góc B cắt AC tại D. Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 3cm, AC= 4cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh \(Dh\perp BC\)
d) So sánh DH với DK
Cho Tam giác ABC vuông tại A, biết AB=6cm, BC=10cm. a)Tính AC. b)Tia phân giác của góc B cắt cạnh AC tại D. Kẻ DE_BC (E-BC). Gọi K là giao điểm của tia ED và đường thẳng AB. Chứng minh: Tam giácABD = Tam giácEBD. c)Chứng minh: Tam giác KDC cân. d) Kẻ AH_CK (H=CK) và tia BD cắt CK tại I. Chứng minh AH song song BI
Câu 6: Cho tam giác ABC có ![]() A = 900, AB = 3cm, AC = 4cm. Tia phân giác của góc B cắt AC tại E. Gọi H là hình chiếu của E trên cạnh BC .
A = 900, AB = 3cm, AC = 4cm. Tia phân giác của góc B cắt AC tại E. Gọi H là hình chiếu của E trên cạnh BC .
a) Tính độ dài cạnh BC.
b) Chứng minh AB = BH
c) Chứng minh : EA < EC
Cho tam giác ABC có A ^ = 120 ° . Tia phân giác của A cắt BC tại D. Tia phân giác của A D C ^ cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB, BC, AD. Chứng minh:
a) AC là tia phân giác của D A H ^ .
b) IH = IK
Cho tam giác ABC có AB AC . Trên tia đối của tia CA lấy điểm D sao cho CD AB . Gọi H , K lần lượt là trung điểm của AD, BC . Trung trực AD, BC cắt nhau tại I. Vẽ IE vuông góc AB tại E .a) Chứng minh Tam giác IABtâm giác IDC và AI là phân giác của BAC .b) Chứng minh BE HC và AI là đường trung trực của đoạn EH .c) Từ C kẻ đường thẳng song song với AB ,cắt đường thẳng EH tại F .Chứng minhTam giác BKE Tam giác CKF và E , K , F thẳng hàng.
vẽ hình hộ mik vs