a)Ta xét trong tam giác ABH có Góc H =90độ
=>BAHˆ+ABHˆ=90
mà BAHˆ+HACˆ=90=A^(gt)
=>ABHˆ=HACˆ
Xét tam giác BHA và Tam giác AIC có:
AB=AC(gt)
H^=AICˆ=90(gt)
ABHˆ=HACˆ(c/m trên)
=>Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn)
=>BH=AI(hai cạnh tương ứng)
b)Vì Tam giác BHA=Tam giác AIC(c/m trên)
=>IC=AH(hai cạnh tương ứng)
Xét trong tam giác vuông ABH có:
BH2+AH2=AB2
mà IC=AH
=>BH2+IC2=AB2(th này là D nằm giữa B và M)
Ta có thể c/m tiếp rằng D nằm giữa M và C thì ta vẫn c/m được Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn) và BH2+IC2=AC2=AB2
=>BH2+CI2 có giá trị ko đổi
c)Ta xét trong tam giác DAC có IC,AM là 2 đường cao và cắt nhau tại N(AM cũng là đường cao do là trung tuyến của tam giác cân xuất phát từ đỉnh và cũng chính là đường cao của đỉnh đó xuống cạnh đáy=>AM vuông góc với DC)
=>DN chính là đường cao còn lại=>DN vuông góc với AC(là cạnh đối diện đỉnh đó)
d)Ta dễ dàng tính được Tam giác DMN cân tại M=>DM=MN(dựa vào số đo của các góc và 1 số c/m trên)
Từ M kẻ đường thẳng ME vuông góc với AD còn MF vuông góc với IC,Ta dễ dàng c/m được tam giác MED=Tam giác MFN(cạnh huyền-góc nhọn)
=>ME=MF(là hai đường vuông góc tại điểm M gióng xuống hai cạnh của góc HICˆ)
Theo tính chất của đường phân giác(Điểm nằm trên đường phân giác của góc này thì cách đều hai cạnh tạo thành góc đó)=>IM là tia phân giác của HICˆ
Đúng 0
Bình luận (1)
Các câu hỏi tương tự
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng:
a) BH = AI.
b) BH^2 + CI^2 = 2AM^2
c) IM là phân giác của góc HIC
Cho tam giác ABC vuông cân tại A, M là trung điểm của BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD.Đường thẳng AM cắt CI tại N.CMR:
a) BH=AI
b) Đường thẳng DN vuông góc với AC
c) IM là tia phân giác của góc HIC
CÓ AI GIÚP EM PHẦN c VỚI NGHĨ MÃI KHÔNG RA
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Ta có tỉ số BC2 / BH2 + CI2 không đổi và có giá trị bằng
Cho tam giác ABC vuông có AB= 6cm, AC= 8cm. Đường phân giác của góc A cắt cạnh BC tại D. Goih M, N theo thứ tự là hình chiêu của B và C trên đường thẳng AD
a, Chứng minh tam giác ABM= Tam giác ACN
b, Tính SABM/SACM
c, Chứng minh AM/AN=DM/DN
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh BC, trên tia đối của tia CB lấy điểm E sao cho CE=BD. Các đường thẳng vuông góc với BC tại D và E lần lượt cắt các đường thẳng AB và Ac theo thứ tự tại M, N. Gọi I là giao điểm của MN với BC. CMR đường thẳng vuông góc với MN luôn đi qua một điểm cố đinh.
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng
∆
đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E, F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng
∆
cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu? A.
a
3
6
4
....
Đọc tiếp
Cho tam giác đều ABC có cạnh bằng a, trên đường thẳng ∆ đi qua A vuông góc với mặt phẳng (ABC) lấy điểm M bất kì. Gọi E, F lần lượt là hình chiếu vuông góc của B lên MC, AC và đường thẳng ∆ cắt EF tại N (như hình bên). Khi đó thể tích của tứ diện MNBC đạt giá trị nhỏ nhất bằng bao nhiêu?
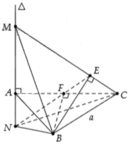
A. a 3 6 4 .
B. a 3 3 4 .
C. a 3 3 6 .
D. a 3 6 12 .
Cho tam giác ABC vuông tại A có AB= 9cm ; BC=10cm
a. Tính AC và so sánh các góc tam giác ABC
b. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm BD. Chứng minh tam giác BCD cân
c. Gọi E; F lần lượt là trung điểm các cạnh DC, BC. Đường thẳng BE cắt cạnh AC tại M.
Tính CM và chứng minh 3 điểm D; M; F thẳng hàng
Cho tam giác ABC đều trên cạnh BC lấy điểm E bất kì đường thẳng vuông góc với AC kẻ từ E cắt đường thẳng vuông góc với AB kẻ từ B tại D lấy trung điểm K của đoạn EC trên tia đối của tia KD lấy điểm F sao cho KD=FK
Từ E kẻ đường thẳng song song với AB cắt AC tại M gọi G là tọng tâm của tam giác CME và I là trung điểm của đoạn MB tính góc AIG
Cho tam giác ABC vuông cân tại A , một đường thẳng d qua A không cắt đoạn AB . K và H là hình chiếu của C và B trên d
a, Chứng minh BH + CK = HK
b, Gọi M là trung điểm BC . Chứng minh tam giác MHK vuông cân
c, Chứng minh diện tích AMBH = diện tích AMCK
đây là toán lớp 8 nha các bạn vẽ hình giùm mik với nha
