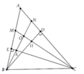
a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.