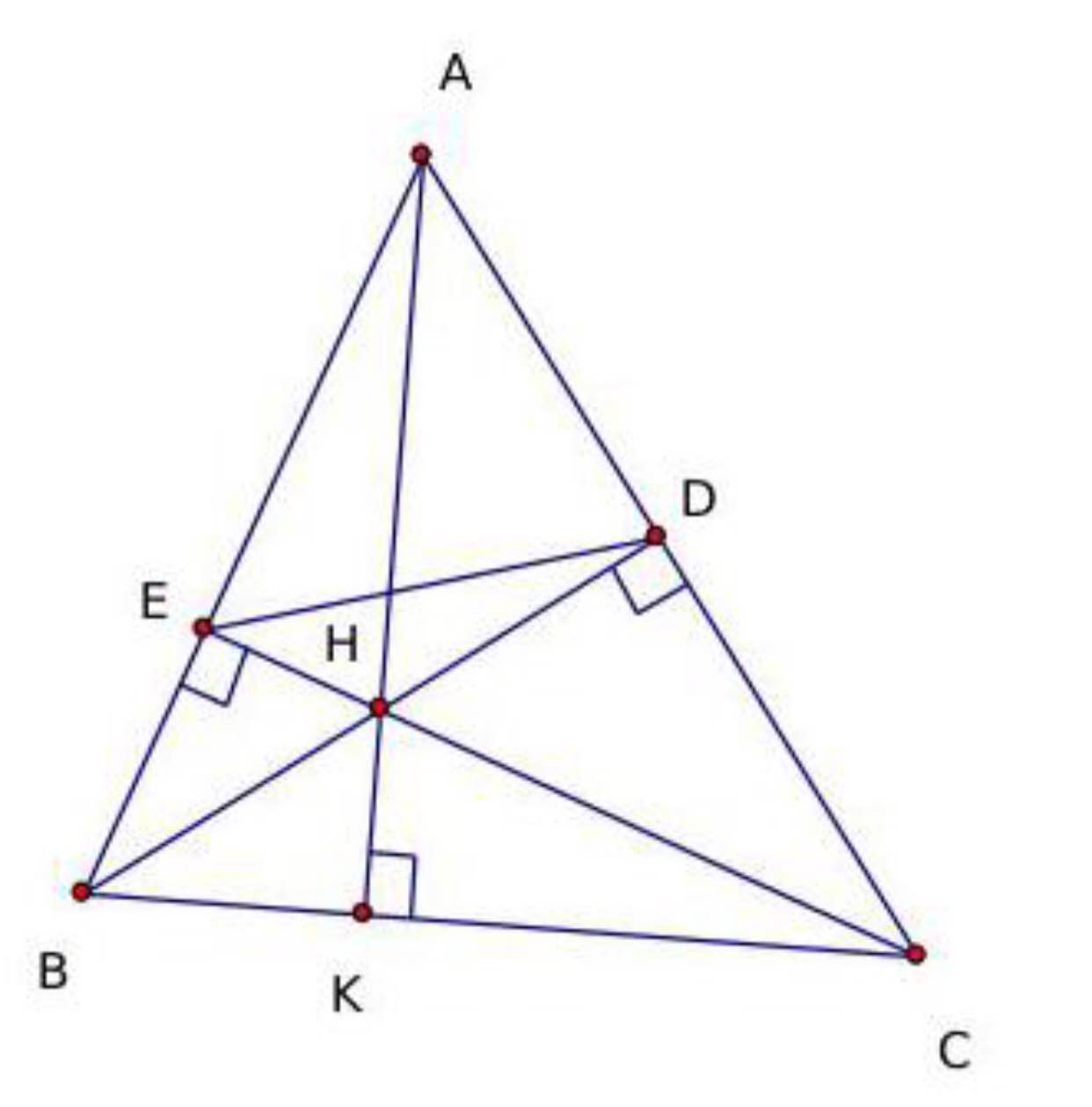
a, Áp dụng định lí Pitago
\(\dfrac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\\ =\dfrac{AK^2+KC^2+\left(BK+KC\right)^2-AB^2}{\left(BK+KC^2\right)+BA^2-\left(AK+KC\right)^2}\\ =\dfrac{2CK^2+2BK.CK}{2BK^2+2BK.Ck}\\ =\dfrac{2CK\left(CK+BK\right)}{2BK\left(BK+CK\right)}=\dfrac{CK}{BK}\)
b, Ta có
\(tanB=\dfrac{AK}{BK};tanC=\dfrac{AK}{CK}\\ Nên:tanBtanC=\dfrac{AK^2}{BK.CK}\left(1\right)\\ Mặt.khác.ta.có:\\ B=HKC\\ mà:tanHKc=\dfrac{KC}{KH}\\ Nên.tanB=\dfrac{KC}{KH}\\ Tương.tự.tanC=\dfrac{KB}{KH}\\ \Rightarrow tanB.tanC=\dfrac{KB.KC}{KH^2}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\left(tanB.tanC\right)^2=\left(\dfrac{AK}{KH}\right)^2\\ Theo.GT:\\ HK=\dfrac{1}{3}AK\Rightarrow tanB.tanC=3\)
c, Chứng minh được
\(\Delta ABC.và.\Delta ADE.đồng.dạng\\ \Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\left(\dfrac{AB}{AD}\right)^2\left(3\right)\)
Mà
\(\widehat{BAC}=60^0\Rightarrow\widehat{ABD}=30^0\\\Rightarrow AB=2AD\left(4\right)\\ Từ.\left(3\right)và\left(4\right)=4\\ \Rightarrow S_{ADE}=30cm^2\)