Cho tam giác ABC ngoại tiếp đường tròn (I). Các cạnh AB, BC, CA tiếp xúc đường tròn (I) lần lượt tại D, E, F. Đặt BC = a, CA = b, AB = c
a, Chứng minh AD =
b
+
c
-
a
2
b, Gọi r là bán kính của (I). Chứng minh S A B C = p.r, trong đó p là nửa chu vi tam giác ABC
c, Gọi M là giao điểm của đoạn thẳng AI với (I). Tính độ dài đoạn thẳng BM theo a, b, c
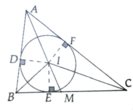
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b

