Cho tam giác $ABC$ không có góc tù $(AB < AC)$, nội tiếp đường tròn $(O; R)$, ($B$, $C$ cố định, $A$ di động trên cung lớn BC). Các tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. Từ $M$ kẻ đường thẳng song song với $AB$, đường thẳng này cắt $(O)$ tại $D$ và $E$ ($D$ thuộc cung nhỏ $BC$), cắt $BC$ tại $F$, cắt $AC$ tại $I$. Chứng minh rằng \(\widehat{MBC}=\widehat{BAC}\) . Từ đó suy ra $MBIC$ là tứ giác nội tiếp.
Cho tam giác không có góc tù , nội tiếp đường tròn , (, cố định, di động trên cung lớn BC). Các tiếp tuyến tại và cắt nhau tại . Từ kẻ đường thẳng song song với , đường thẳng này cắt tại và ( thuộc cung nhỏ ), cắt tại , cắt tại . Chứng minh rằng . Từ đó suy ra là tứ giác nội tiếp.
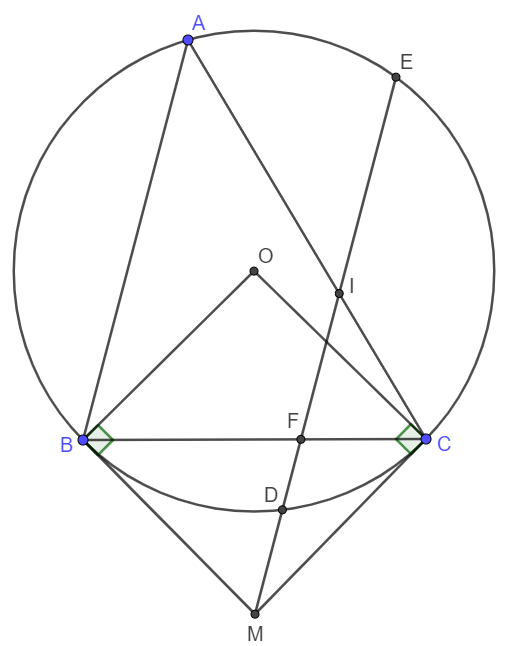
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep
