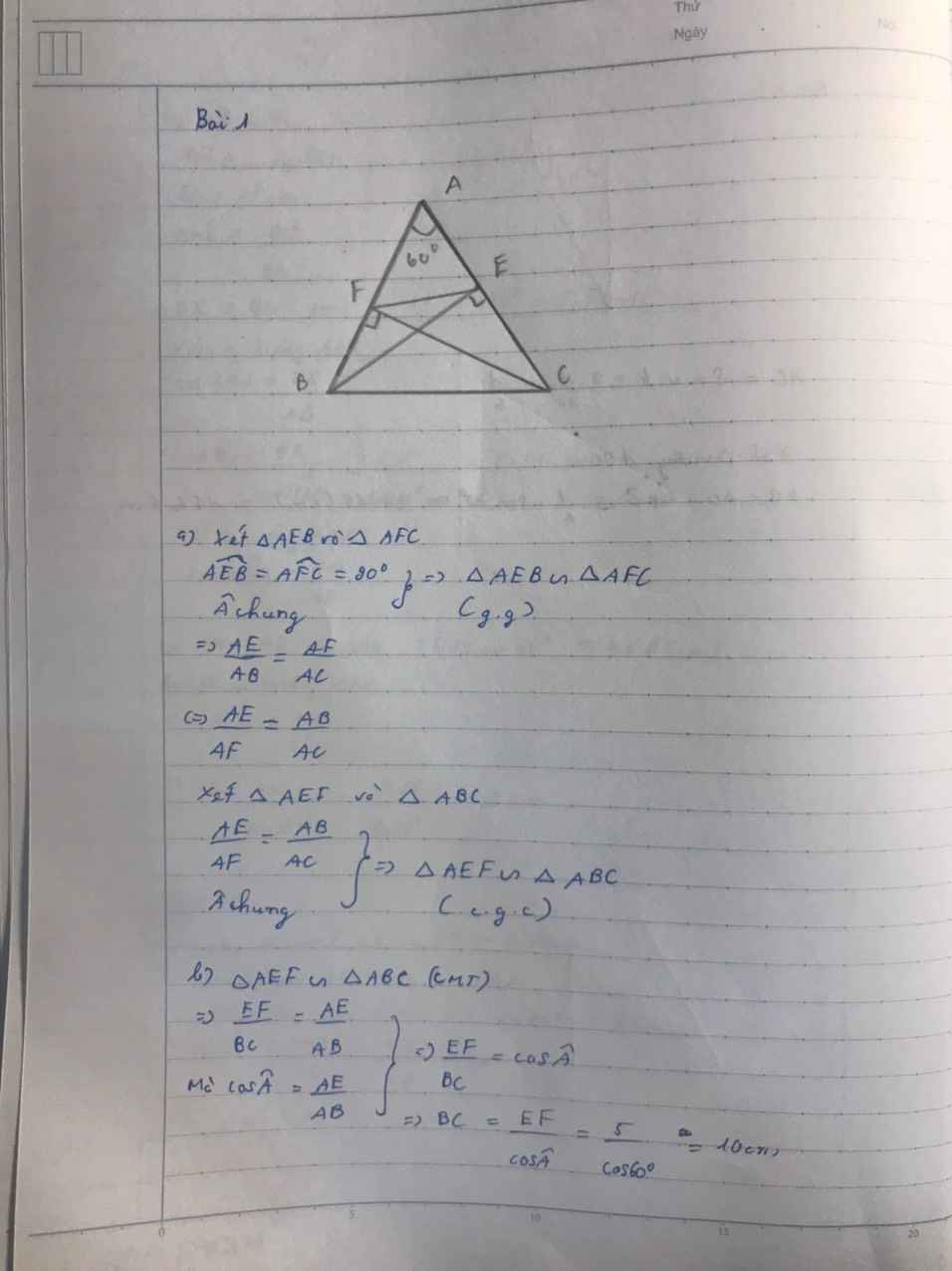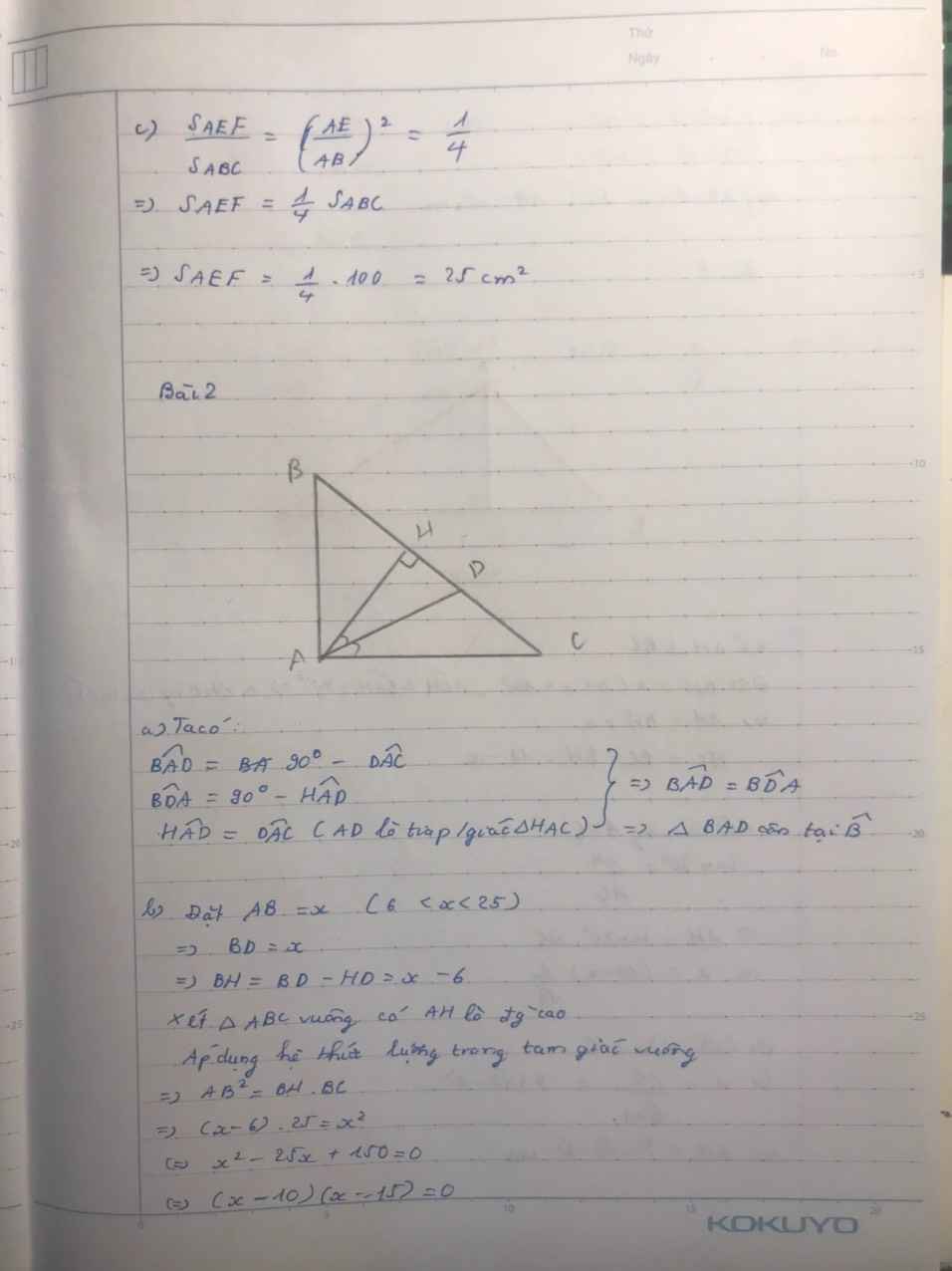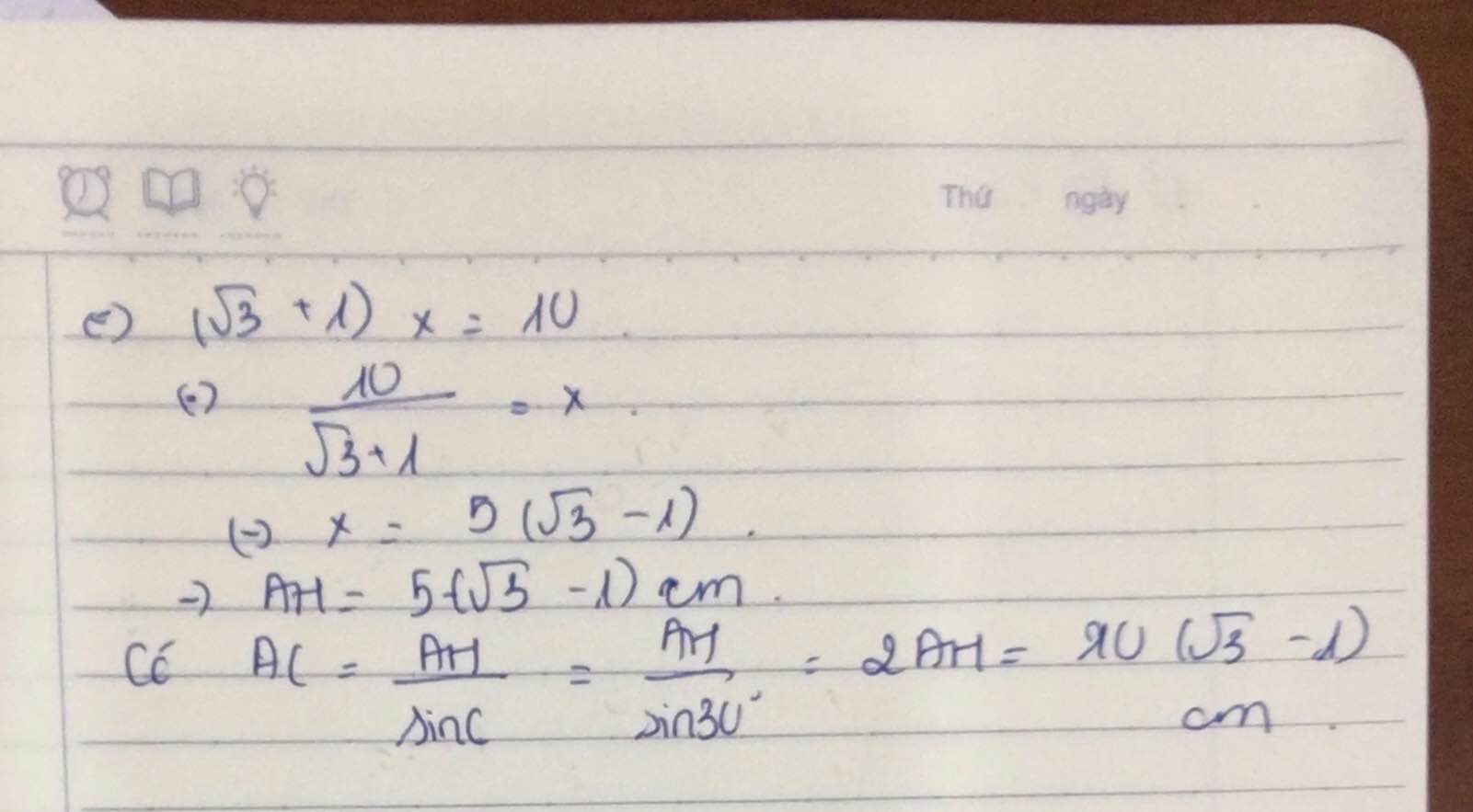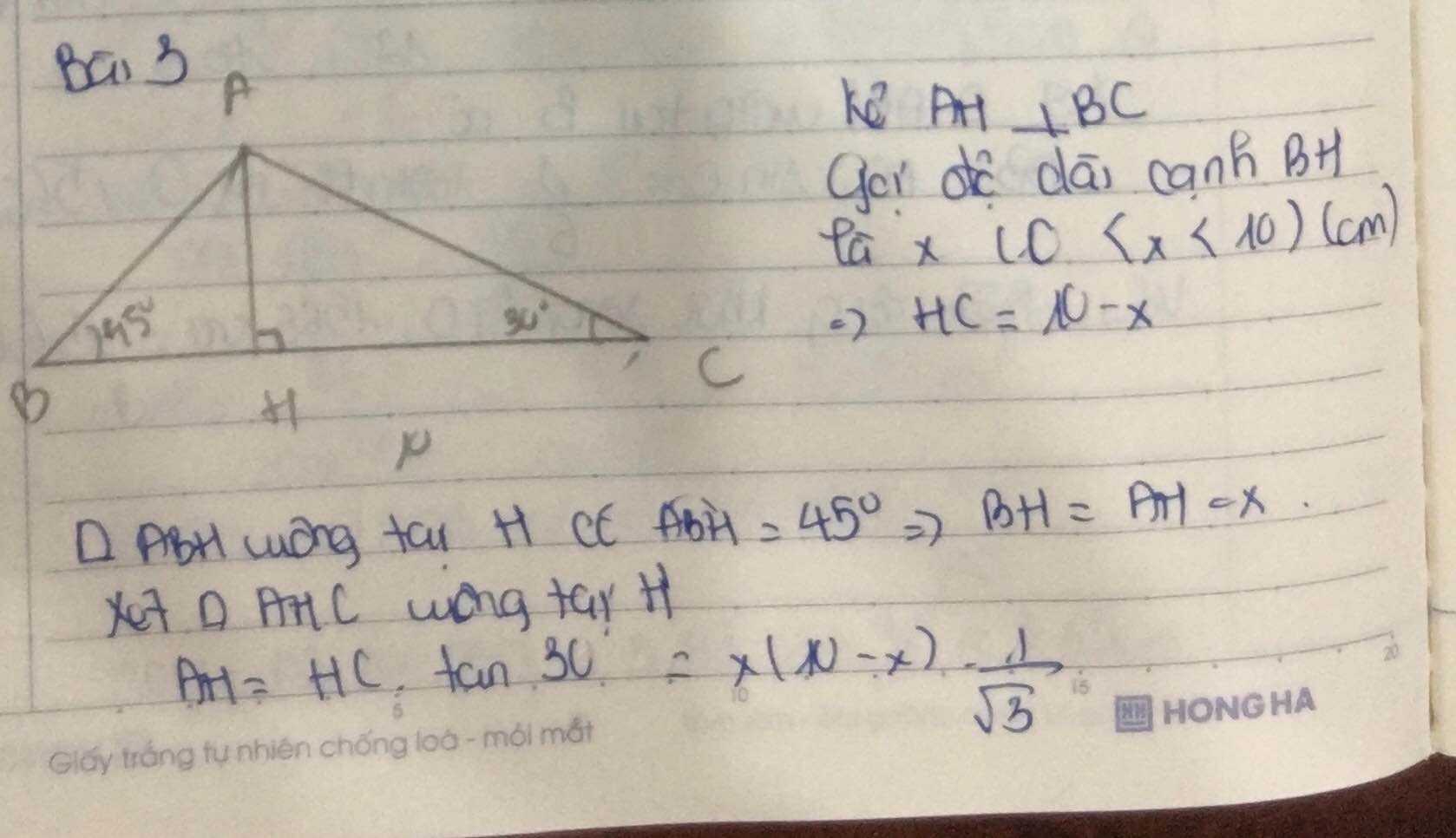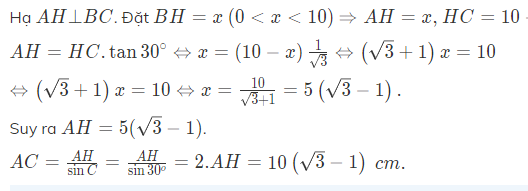Trả lời:
Tam giác ABC có:
Sin B = AC/BC (hệ thức lượng)
=> AC = Sin B.BC = Sin 450 . 10 = 5√2 (cm)
Sin C = AB/BC
=> AB = Sin 300 . 10 = 5 (cm)
Ta có tam giác ABC có: góc A + góc B + góc C = 1800
=> góc A = 1800 - 450 - 300 = 1050
Tam giác ABC có: Sin B = (hệ thức lượng) => AC = Sin B.BC = Sin 450 . 10 = (cm)
Sin C = (hệ thức lượng) => AB = Sin 300 . 10 = 5 (cm)
Ta có tam giác ABC có: góc A + góc B + góc C = 1800 (định lý)
=> góc A = 1800 - 450 - 300 = 1050
Kẻ AH vuông góc với BC. Đặt BH=x (0<x<10)
\(\Rightarrow\) AH=x , HC=10-x
AH=HC.tan \(30^0\)\(\Leftrightarrow x=\left(10-x\right).\dfrac{1}{\sqrt{3}}\Leftrightarrow\left(\sqrt{3}+1\right).x=10\)
\(\Rightarrow AH=5.\left(\sqrt{3}-1\right)\)
AC=\(\dfrac{AH}{\sin C}=\dfrac{AH}{\sin30^0}=2.AH=10.\left(\sqrt{3}-1\right)cm\)
Áp dụng định lý Pytago vào\(\Delta ABC\) ta có:
AB=\(\sqrt{BC^2-AC^2}=\sqrt{10^2-[10.\left(\sqrt{3}-1\right)]^2}\approx6,813cm\)
Vậy AC=10.(\(\sqrt{3}\)-1); AB\(\approx\)6,813cm
Hạ . Đặt .
Suy ra .
Hạ . Đặt .
Suy ra .
Hạ . Đặt .
Suy ra .
Hạ AH vuông vs BC. Đặt BH= x(0<x<10) ⇒AH=x, HC= 10-x
AH=HC.\(\tan30^o\)⇔ x= ( 10 - x ) . \(\dfrac{1}{\sqrt{3}}\)⇔(\(\sqrt{3}\)+1)x= 10 ⇔ x= \(\dfrac{10}{\sqrt{3}+1}\)= 5(\(\sqrt{3}\)- 1)
⇒AH= \(5\left(\sqrt{3}-1\right)\)
AC = \(\dfrac{AH}{\sin C}=\dfrac{AH}{\sin30^O}=2.AH=10\left(\sqrt{3}-1\right)\)cm
AC=5\(\sqrt{2}\)cm
AB=5cm
Hạ . Đặt .
Suy ra .
Kẻ AH vuông góc với BC. Đặt BH=x
ð AH=x ; HC=10-x
AH=HC. Tan30
ó(căn 3+1)x=(10-x).1/căn3 ó(căn 3+1)x=10
óx= 5(căn 3-1)
ð AH=5(căn 3-1)
AC=AH/sinC=AH/sin30=2.AH=10(căn 3-1) cm
AH= 5( căn 3 -1)
AC = 10( căn 3 - 1)
Các câu hỏi tương tự
Cho tam giác $ABC$ có ba góc nhọn, $\hat{A}={60}^\circ$. Kẻ hai đường cao $BE$ và $CF$.
a) Chứng minh $\Delta AEF\backsim\Delta ABC$;
b) Cho $EF=5cm$, tính $BC$.
c) Cho $S_{ABC}=100 cm^2$.Tính $S_{AEF}$.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi AD là phân giác trong của tam giác AHC.
a) Chứng minh tam giác BAD là tam giác cân;
b) Cho BC = 25cm, HD = 6cm. Tính AB.





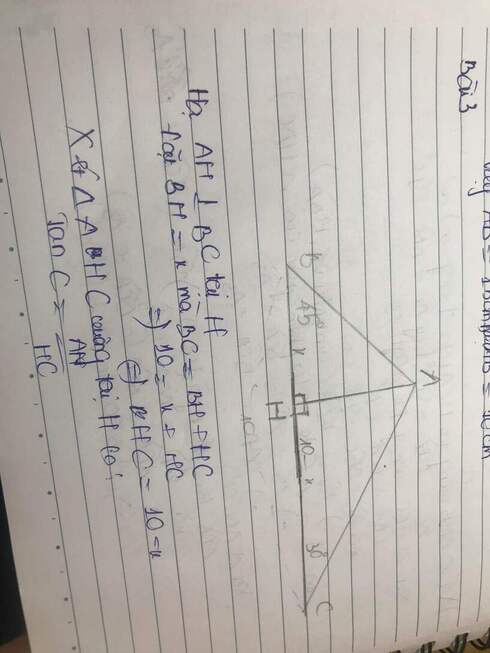
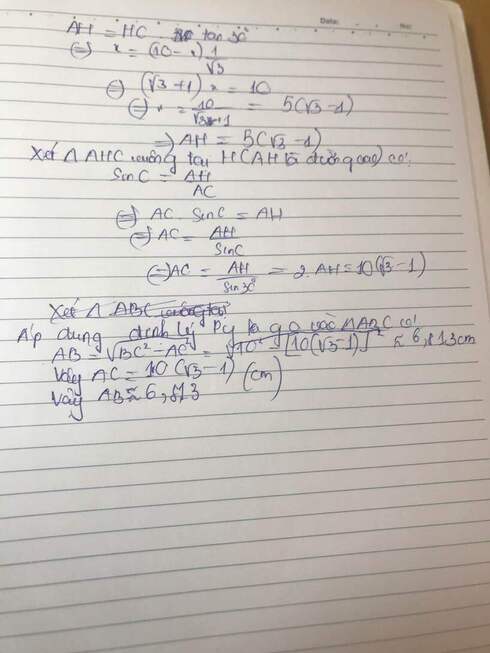

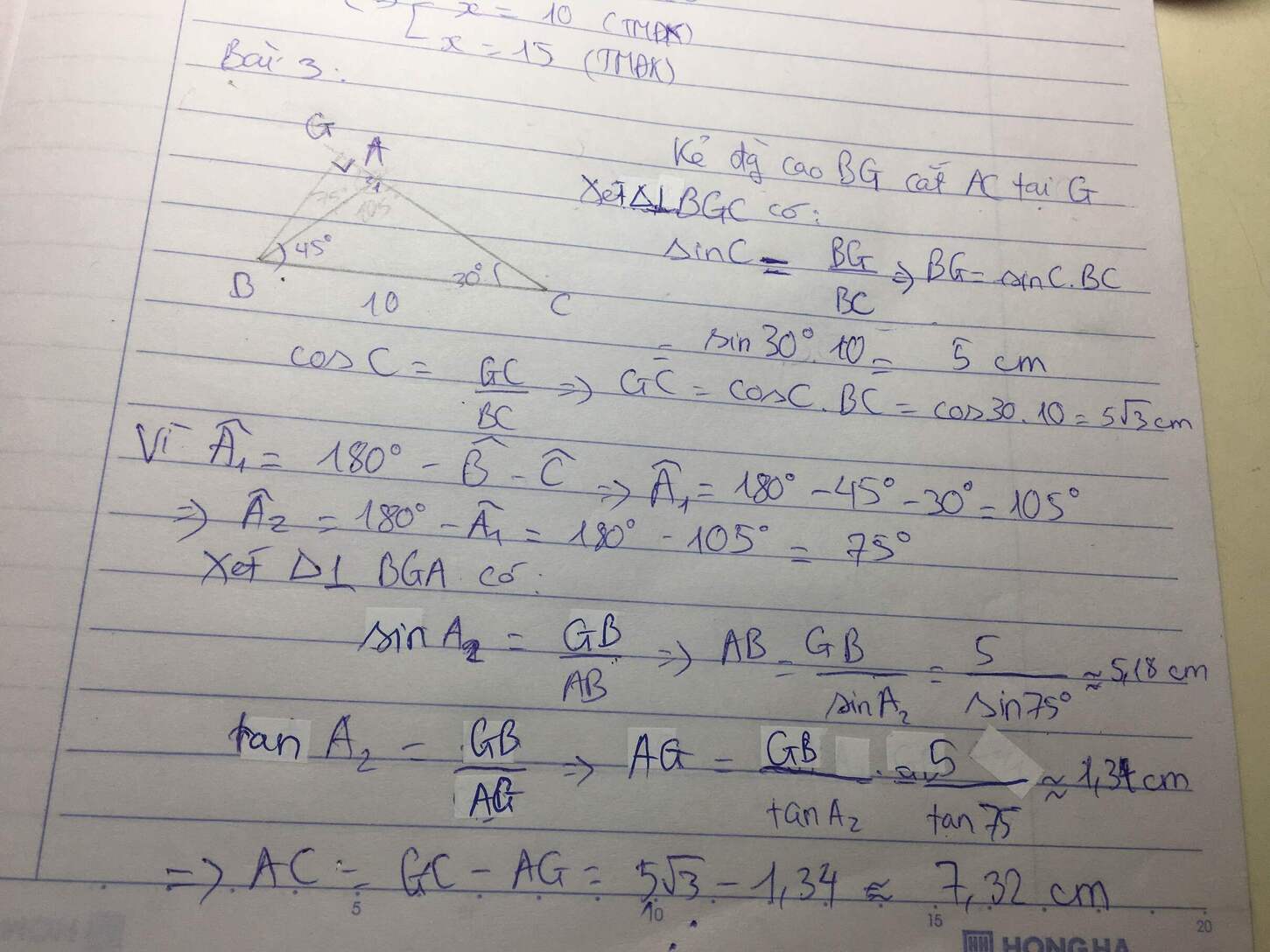

 .jpg)
 .jpg)