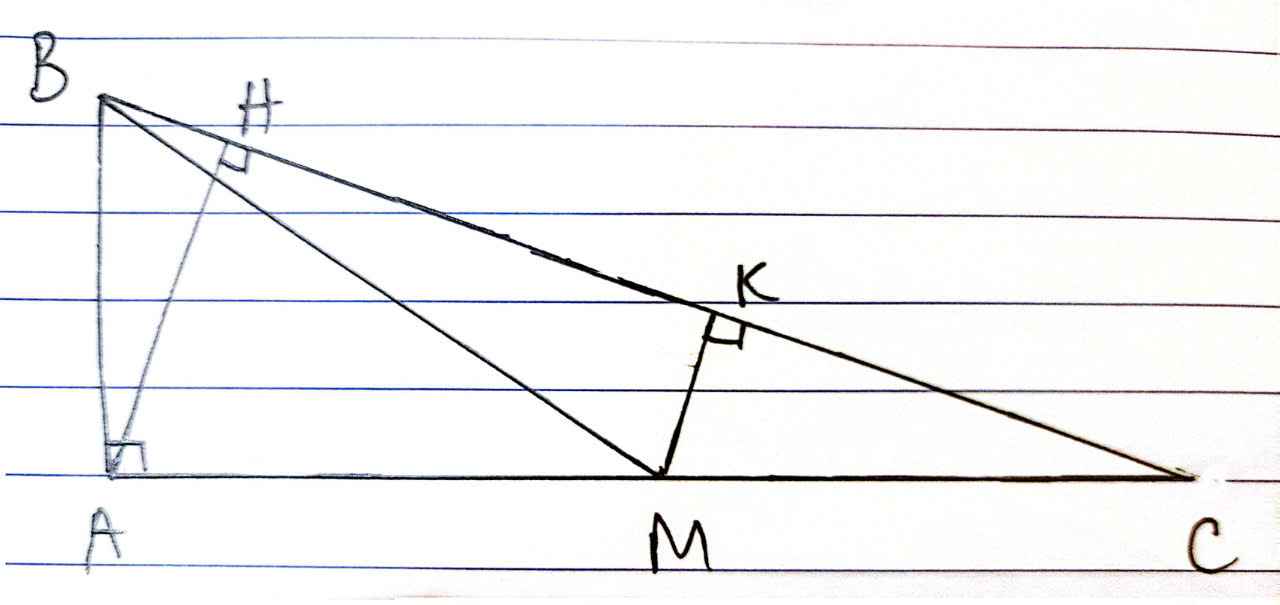
a. \(\Delta ABC\) vuông tại A có sinC = \(\dfrac{AB}{BC}=\dfrac{1}{3}\Rightarrow BC=3AB=3.6=18\left(cm\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{18^2-6^2}=12\sqrt{2}\left(cm\right)\) (định lý Pytago)
Theo hệ thức lượng trong tam giác vuông:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{18}=\dfrac{36}{18}=2\left(cm\right)\)
\(\Rightarrow HC=BC-BH=18-2=16\left(cm\right)\)
b. M là trung điểm AC => \(MC=\dfrac{AC}{2}=\dfrac{12\sqrt{2}}{2}=6\sqrt{2}\left(cm\right)\)
\(\Delta MKC\) vuông tại K có sinC = \(\dfrac{MK}{MC}=\dfrac{1}{3}\Rightarrow MK=3MC=3.6=18\sqrt{2}\left(cm\right)\)
c. \(\Delta ABM\) vuông tại A có \(MB=\sqrt{AB^2+AM^2}=\sqrt{6^2+\left(6\sqrt{2}\right)^2}=6\sqrt{3}\left(cm\right)\)
\(\Delta MKB\) vuông tại K có \(tan\widehat{KBM}=\dfrac{MK}{MB}=\dfrac{18\sqrt{2}}{6\sqrt{3}}=\sqrt{6}\Rightarrow\widehat{KBM}hay\widehat{MBC}\approx67^o47^,\)