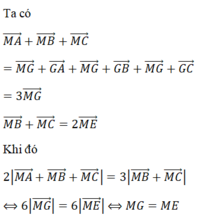
Suy ra tập họp các điểm M cần tìm là đường trung trực của đoạn GE.
Đáp án B
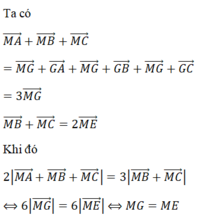
Suy ra tập họp các điểm M cần tìm là đường trung trực của đoạn GE.
Đáp án B
Trong hệ tọa độ Oxy, cho tam giác ABC có C (-2; -4), trọng tâm G(0; 4) và trung điểm cạnh BC là M (2; 0). Tổng hoành độ của điểm A và B là?
A. -2
B. 2
C. 4
D. 8
Cho ba điểm A (0,6) B(-3,2) C(5,-1)
A ) chứng minh rằng A , B ,C lập thành một tam giác
B ) Tìm tọa độ điểm M ,N , P lần lượt là trung điểm của AB , BC và CA
C ) Tìm tọa độ điểm D sao cho A là trọng tâm tam giác BCD
D ) Tìm tọa độ điểm E sao cho tứ giác ABEC là hình bình hành
Cho tam giác ABC, A(4;0) B(2;-4) C(0;-2). Gọi G là trọng tâm tam giác ABC. GỌi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Chứng minh tam giác ABC, tam giác MNP có cùng trọng tâm
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).
a/ Tìm tọa độ trọng tâm G của tam giác ABC.
b/ Tìm tọa độ điểm D để ABCD là hình bình hành
c/ Tìm tọa độ ![]() sao cho
sao cho ![]()
Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng: 
Các điểm M(2;3). N(0;-4), P(-1;6) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC.
a)Tìm tọa độ đỉnh A,B,C của Tam giác.
b) C/m tam giác ABC và MNP có cùng trọng tâm
Tam giác ABC có C(–2; –4), trọng tâm G(0; 4), trung điểm cạnh BC là M(2; 0). Tọa độ điẻm A và B là:
A. A(4; 12) , B(4; 6)
B. A(–4; –12), B(6; 4)
C. A(–4; 12), B(6; 4)
D. A(4; –12), B(–6; 4)
Cho tam giác ABC Gọi M là trung điểm của AB có G là trọng tâm,I là trung điểm của AB ,M thuộc AB sao cho vtMA+3vtMB=vt0.
a) Phân tích vecto MG theo hai vecto MC và MB.
Cho tam giác ABC có trọng tâm G. M, N lần lượt là trung điểm của AB, BC. Lấy 2 điểm I, J sao cho \(2\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{0}\), \(2\overrightarrow{JA}+5\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\)
a) CM: M, N, J thẳng hàng với J là trung điểm của BI
b) Gọi E là điểm thuộc AB sao cho \(\overrightarrow{AE}=k.\overrightarrow{AB}\). Xác định k sao cho C, E, J thẳng hàng
Câu 1: cho tam ABC. Có bao nhiêu điểm M thỏa mãn | vecto MA+vectoMB+vectoMC| = 3
a.1
b.2
c.3
d. vô số
Câu 2: cho tam giác ABC đều cạnh a. biết rằng tập hợp các điểm M thỏa mãn đẳng thức |2vectoMA+3vectoMB+4vectoMC|=|vectoMB-vectoMA| là đường tròn cố định có bán kính R. tính bán kính R theo A?
Câu 3: Cho 2 điểm A.B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức |2vectoMA+vectoMB|=|vectoMA+2vectoMB| là:
a. đường trung trực của đoạn thẳng AB
b. đường tròn đường kính AB
c. đường trung trực của đoạn thẳng IA
d. đường tròn tâm A, bán kính AB