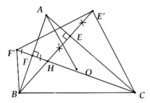
Cho tam giác ABC có hai đường cao BE, CF cắt nhau tại H. Gọi E' là điểm đối xứng H qua AC, F' là điểm đối xứng H qua AB. Chứng minh:
a, Tứ giác BCE'F' nội tiếp đường tròn (O)
b, Năm điểm A, F', B, C, E' cùng thuộc một đường tròn
c, AO và EF vuông góc nhau
d, Khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không đổi
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi

