Question

 Cho tam giác ABC có hai đường cao AD và BE cắt nhau tại H. Tia CH cắt AB tại K. Kẻ DM vuông góc AB tại M, từ M vẽ đường thẳng song song với KE cắt AC tại N. Chứng minh DN vuông góc AC

Answer 1

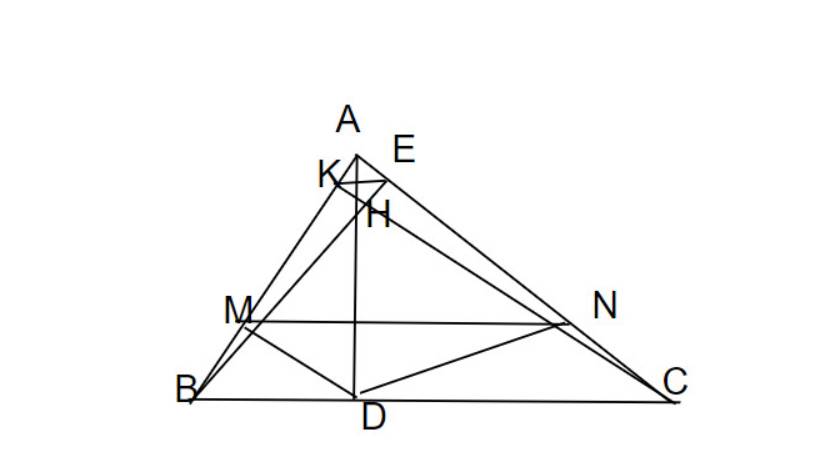
xét ΔAKH và Δ AMD, có

\(\widehat{A}=\widehat{A}\\ \widehat{K}=\widehat{M}=90^o\\ \Rightarrow\text{ }\Delta AKH\sim\Delta AMD\left(g-g\right)\)

\(\Leftrightarrow\dfrac{AH}{AD}=\dfrac{AK}{AM}\)(1)

xét ΔAKE và Δ AMN, có:

\(\widehat{A}\) chung

\(\widehat{E}=\widehat{N}\) đồng vị

\(\Rightarrow\text{ }\Delta AKE\sim\Delta AMN\left(g-g\right)\)

\(\Leftrightarrow\dfrac{AE}{AN}=\dfrac{AK}{AD}\)(2)

xét ΔAHE và Δ ADN, có:

\(\widehat{A}\) chung 

từ (1) và (2) ta suy ra \(\dfrac{AH}{AD}=\dfrac{AE}{AN}\\ \Rightarrow\Delta AHE~\Delta ADN\)

\(\Leftrightarrow\widehat{E}=\widehat{N}=90^o\Rightarrow DN\perp AC\left(đpcm\right)\)

P/S: chúc bạn học tốt nhe, mình vẽ hình xong nhìn muốn nội thương=))