a, Chứng minh IFEK là hình bình hành có tâm O. Chứng minh IK ⊥ KE => IFEKlà hình chữ nhật => I,F,E,K cùng thuộc (O;OI)
b, Ta có: I D E ^ = 90 0 => Tam giác IDE vuông tại D
Chứng minh rằng KD ⊥ DF => ∆ KDF vuông
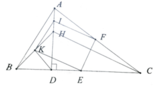
cho tam giác ABC đường cao AD , trực tâm H ,gọi I ,K theo thứ tự là trung điểm của HA, HB .Gọi E , F theo thứ tự là trung điểm của BC , AC . Chứng minh rằng :
a) 4 điểm E, F , I , K cùng thuộc một đường tròn
b) điểm D thuộc đường tròn đó
Cho tam giác ABC, đường cao AD, trực tâm H. Gọi I,K lần lượt là trung điểm của HA, HB. E,F lần lượt là trung điểm của BC,AC. Chứng minh 5 điểm D,E,F,I,K cùng thuộc một đường tròn
Cho tam giác ABC nội tiếp đường tròn (O). M là một điểm trên cung BC không chứa A. Gọi. D, E, F lần lượt là hình chiếu của M trên BC, AC và AB
a) Chứng minh rằng D, E, F thẳng hàng.
b) Gọi I, J, K lần lượt là các điểm đối xứng của M qua D, E, F. Chứng minh rằng I, J, K cùng thuộc một đường thẳng và đường thẳng đó đi qua trực tâm H của tam giác ABC.
Cho tam giác ABC có D,E,F lần lượt là trung điểm của BC,CA,AB. G,H,I lần lượt là chân đường cao hạ từ đỉnh A,B,C. Trực tâm tam giác ABC là S. J,K,L theo thứ tự là trung điểm SA,SB,SC. Chứng minh rằng: 9 Điểm D,E,F,G,H,I,L,K,J cùng thuộc đường tròn. (Gợi ý: đường tròn đường kính JD)
Cho tam giác ABC có 3 góc nhọn nội tiếp (O). Vẽ các đường cao AD, BE, CF cắt nhau tại H. a/ Chứng mính bốn điểm C, D, ,H,E cùng thuộc một đường tròn tâm I. b/ Chứng minh bốn điểm B, F,E,C cùng thuộc một đường tròn tâm K. c/ Gọi M là trung điểm AH. Chứng minh: góc MEK = 90⁰
Một số bài toán hay về tâm nội tiếp:
Bài 1: Cho tam giác ABC nội tiếp (O), hai điểm K,L di chuyển trên (O) (K thuộc cung AB không chứa C, L thuộc cung AC không chứa B) thỏa mãn KL song song với BC. Gọi U và V lần lượt là tâm nội tiếp các tam giác AKB,ALC. Chứng minh rằng tâm của (UAV) thuộc đường thẳng cố định.
Bài 2: Cho tứ giác lồi ABCD có AD = BC. AC cắt BD tại I. Gọi S,T là tâm nội tiếp các tam giác AID,BIC. M,N là trung điểm các cạnh AB,CD. Chứng minh rằng MN chia đôi ST.
Bài 3: Cho tam giác ABC, đường tròn (I) nội tiếp tam giác ABC tiếp xúc BC,CA,AB tại D,E,F. Kẻ DH vuông góc EF tại H, G là trung điểm DH. Gọi K là trực tâm tam giác BIC. Chứng minh rằng GK chia đôi EF.
Bài 4: Cho tam giác ABC ngoại tiếp (I), (I) tiếp xúc với BC,CA,AB tại D,E,F. Gọi AI cắt DE,DF tại K,L; H là chân đường cao hạ từ A của tam giác ABC, M là trung điểm BC. Chứng minh rằng bốn điểm H,K,L,M cùng thuộc một đường tròn có tâm nằm trên (Euler) của tam giác ABC.
Cho \(\Delta\) ABC, đường cao AD, H là trực tâm. Gọi I,K thứ tự là trưng điểm của AH, AB. Gọi E,F thứ tự là trung điểm của BC,AC
a) 4 điểm E,F,I,K thuộc 1 đường tròn
b) D cũng thuộc đường tròn đó.
Cho đường tròn(O:R), dây AB cố định không đi qua tâm O. Lấy điểm M thuộc tia đối của tia BA. Kẻ tiếp tuyến ME, MF (E, F thuộc (O)). Gọi H là trung điểm AB.
1) Chứng minh: 5 điểm H, E, O, M F thuộc một đường tròn.
2) Gọi I, K lần lượt là giao điểm của EF với OH ; OM. Chứng minh: OH. OI = OK.OM.
3) Chứng minh: IA và IB là tiếp tuyến của đường tròn (O) và EF luôn đi qua một điểm cố định khi M chuyển động trên tia đối của tia BA.
cho tam giác ABC, 3 đường cao AD,BE,CF cắt nhau tại H. I,K,L là trung điểm AB,BC,AC. M,N,P là trung điểm HA,HB,HC. cm 9 điểm D,E,F,L,I,K,M,N,P cùng thuộc một đường tròn
