Chọn B.
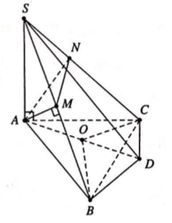
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, và D là điểm đối xứng với A qua O.
Ta có BD ⊥ AB (góc nội tiếp chắn nửa đường tròn).
Và BD ⊥ SA ⇒ BD ⊥ ( SAB ) ⇒ BD ⊥ AM .
Mặt khác AM ⊥ SB ⇒ AM ⊥ ( SBD ) ⇒ SD ⊥ AM .
Chứng minh tương tự ta được SD ⊥ AN ⇒ SD ⊥ ( AMN ) .
Ta có SD ⊥ ( AMN ) SA ⊥ ( ABC ) ⇒ ( ( AMN ) ; ( ABC ) ^ )
= ( SA ; SD ^ ) = ASD ^ .
Ta có: AD = 2 R ABC = BC sin A ^ = a 2
Vậy ( ( AMN ) ; ( ABC ) ^ ) = ASD ^ = arctan 1 = 45 o

