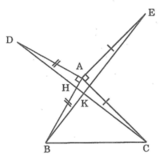
Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K
Ta có: ΔABE = ΔADC (cmt)
⇒ ∠ABE = ∠ADC (hai góc t.ư)
hay ∠HBK = ∠ADH
+ ΔADH và ΔBKH đều có tổng ba góc trong mỗi tam giác bằng 180o nên có:
∠ADH + ∠DAH + ∠AHD = ∠BKH + ∠KHB + ∠HBK
Mà ∠AHD = ∠BHK (hai góc đối đỉnh)
∠ADH = ∠HBK (chứng minh trên)
Suy ra ∠DAH = ∠HKB
Mà ∠DAH = 90o nên ∠HKB = 90o
⇒ DC ⊥ BE (điều phải chứng minh)

