B1: Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.
a) Chứng minh tứ giác AEHF là hình chữ nhật
b) Chứng minh tứ giác BEFC nội tiếp
c) Gọi I là trung điểm của B
C.Chứng minh AI vuông góc với EF
d) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEF
C.Tính diện tích hình tròn tâm K.
B2: Cho ABC nhọn, đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và D, CE cắt BD tại H
a) Chứng minh tứ giác ADHE nội tiếp
b) AH cắt BC tại F. chứng minh FA là tia phân giác của góc DFE
c) EF cắt đường tròn tại K ( K khác E). chứng minh DK// AF
d) Cho biết góc BCD = 450 , BC = 4 cm. Tính diện tích tam giác ABC
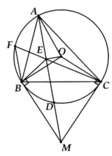
B 3: cho đường tròn ( O) và điểm A ở ngoài (O)sao cho OA = 3R. vẽ các tiếp tuyến AB, AC với đường tròn (O) ( B và C là hai tiếp tuyến )
a) Chứng minh tứ giác OBAC nội tiếp
b) Qua B kẻ đường thẳng song song với AC cắt ( O) tại D ( khác B). đường thẳng AD cắt ( O) tại E. chứng minh AB2= AE. AD
c) Chứng minh tia đối của tia EC là tia phân giác của góc BEA
d) Tính diện tích tam giác BDC theo R
B4: Cho tam giác ABC nhọn, AB >AC, nội tiếp (O,R), hai đường cao AH, CF cắt nhau tại H
a) Chứng minh tứ giác BDHF nội tiếp? Xác định tâm của đường tròn ngoại tiếp tứ giác đó
b) Tia BH cắt AC tại E. chứng minh HE.HB= HF.HC
c) Vẽ đường kính AK của (O). chứng minh AK vuông góc với EF
d) Trường hợp góc KBC= 450, BC = R. tính diện tích tam giác AHK theo R
B5: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Ba đương cao AE, BF, CK cắt nhau tại H. Tia AE, BF cắt đường tròn tâm O lần lượt tại I và J.
a) Chứng minh tứ giác AKHF nội tiếp đường tròn.
b) Chứng minh hai cung CI và CJ bằng nhau.
c) Chứng minh hai tam giác AFK và ABC đồng dạng với nhau
B6: Cho tam giác ABC nhọn nội tiếp đường tròn ( O; R ),các đường cao BE, CF .
a)Chứng minh tứ giác BFEC nội tiếp.
b)Chứng minh OA vuông góc với EF.