a, Ta có A C M ^ = 90 0 (góc nội tiếp)
b, Ta có ∆ABH:∆AMC(g.g)
=> B A H ^ = O A C ^ ; O C A ^ = O A C ^
=> B A H ^ = O C A ^
c, A N M ^ = 90 0
=> MNBC là hình thang
=> BC//MN => sđ B N ⏜ = sđ C M ⏜
=> C B N ^ = B C M ^ nên BCMN là hình thang cân
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
AP
23 tháng 1 2022 lúc 21:08
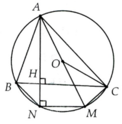
Cho tam giác ABC có ba góc nhon, đường cao AH và nội tiếp đường tròn tâm O, đường kính AM.
a) tính góc ACM
b) Chứng minh góc BAH=góc OCA
c) Gọi N là giao điểm AH với đường tròn (O). Tứ giác BCMN là hình gì ? Vì sao?
1/ Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R) H là giao điểm 2 đường cao BD,CE của tam giác ABC
a) Chứng minh tứ giác BCDE nội tiếp. Xác định tâm đường tròn
b) F là giao điểm AH,BC. Vẽ đường kính AK của đường tròn (O). Chứng minh góc AFB=góc ACK
c) Chứng minh tứ giác BHCK là hình bình hành và H,I,K thẳng hàng
B1: Cho tam giác ABC vuông tại A, biết AB 6cm, AC 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.a) Chứng minh tứ giác AEHF là hình chữ nhậtb) Chứng minh tứ giác BEFC nội tiếpc) Gọi I là trung điểm của BC.Chứng minh AI vuông góc với EFd) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEFC.Tính diện tích hình tròn tâm K.B2: Cho ABC nhọn, đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và D, CE cắt BD tại Ha) Chứng minh tứ giác ADHE nội tiếpb) AH cắ...
Đọc tiếp
B1: Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.
a) Chứng minh tứ giác AEHF là hình chữ nhật
b) Chứng minh tứ giác BEFC nội tiếp
c) Gọi I là trung điểm của B
C.Chứng minh AI vuông góc với EF
d) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEF
C.Tính diện tích hình tròn tâm K.
B2: Cho ABC nhọn, đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và D, CE cắt BD tại H
a) Chứng minh tứ giác ADHE nội tiếp
b) AH cắt BC tại F. chứng minh FA là tia phân giác của góc DFE
c) EF cắt đường tròn tại K ( K khác E). chứng minh DK// AF
d) Cho biết góc BCD = 450 , BC = 4 cm. Tính diện tích tam giác ABC
B 3: cho đường tròn ( O) và điểm A ở ngoài (O)sao cho OA = 3R. vẽ các tiếp tuyến AB, AC với đường tròn (O) ( B và C là hai tiếp tuyến )
a) Chứng minh tứ giác OBAC nội tiếp
b) Qua B kẻ đường thẳng song song với AC cắt ( O) tại D ( khác B). đường thẳng AD cắt ( O) tại E. chứng minh AB2= AE. AD
c) Chứng minh tia đối của tia EC là tia phân giác của góc BEA
d) Tính diện tích tam giác BDC theo R
B4: Cho tam giác ABC nhọn, AB >AC, nội tiếp (O,R), hai đường cao AH, CF cắt nhau tại H
a) Chứng minh tứ giác BDHF nội tiếp? Xác định tâm của đường tròn ngoại tiếp tứ giác đó
b) Tia BH cắt AC tại E. chứng minh HE.HB= HF.HC
c) Vẽ đường kính AK của (O). chứng minh AK vuông góc với EF
d) Trường hợp góc KBC= 450, BC = R. tính diện tích tam giác AHK theo R
B5: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Ba đương cao AE, BF, CK cắt nhau tại H. Tia AE, BF cắt đường tròn tâm O lần lượt tại I và J.
a) Chứng minh tứ giác AKHF nội tiếp đường tròn.
b) Chứng minh hai cung CI và CJ bằng nhau.
c) Chứng minh hai tam giác AFK và ABC đồng dạng với nhau
B6: Cho tam giác ABC nhọn nội tiếp đường tròn ( O; R ),các đường cao BE, CF .
a)Chứng minh tứ giác BFEC nội tiếp.
b)Chứng minh OA vuông góc với EF.
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Gọi D,E,K lần lượt là chân đường cao kẻ từ A,B,C của tam giác ABC . H là trực tâm của tam giác ABC
a,CM: tứ giác HDCE nội tiếp
b, Gọi M là giao điểm của AH và (O). Chứng minh D là trung điểm của HM
c,Chứng minh: OA vuông góc với EK
BT1: Cho tam giác ABC ( AB AC) nội tiếp đường tròn tâm O . Ba đường cao AH, BE, CF cắt nhau tại I. Kẻ đường kính AD của đường tròn O, gọi M là trung điểm BC.a/ Chứng minh: 4 điểm B, F, E, C cùng nằm trên một đường trònb/ Chứng minh : EF BCc/ Tứ giác BICD là hình gì ? Vì sao ?d/ Chứng minh : OM AI / 2BT2: Cho đường tròn tâm O, điểm A nằm ngoài đường tròn. Từ A vẽ hai đường thẳng cắt đường tròn, đường thứ nhất cắt đường tròn tại M và N ( M nằm giữa A và N ), đường thứ 2 cắt đường tròn tại E và F...
Đọc tiếp
BT1: Cho tam giác ABC ( AB< AC) nội tiếp đường tròn tâm O . Ba đường cao AH, BE, CF cắt nhau tại I. Kẻ đường kính AD của đường tròn O, gọi M là trung điểm BC.
a/ Chứng minh: 4 điểm B, F, E, C cùng nằm trên một đường tròn
b/ Chứng minh : EF < BC
c/ Tứ giác BICD là hình gì ? Vì sao ?
d/ Chứng minh : OM = AI / 2
BT2: Cho đường tròn tâm O, điểm A nằm ngoài đường tròn. Từ A vẽ hai đường thẳng cắt đường tròn, đường thứ nhất cắt đường tròn tại M và N ( M nằm giữa A và N ), đường thứ 2 cắt đường tròn tại E và F ( E nằm giữa A và F ) sao cho MN = EF. Kẻ OH vuông góc MN, OK vuông góc EF.
a/ So sánh AH và AK
b/ Chứng minh : AM = AE
c/ Tứ giác MEFN là hình gì ? Vì sao ?
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Kẻ đường cao AH và đường kính AD. Gọi M và N lần lượt là hình chiếu vuông góc của B và C trên AD. Chứng minh rằng tam giác ABC đồng dạng với tam giác HMN và trung điểm I của cạnh BC cũng là tâm đường tròn ngoại tiếp tam giác HMN.
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao BD, CE của tam giác ABC cắt nhau tại H. a) Chứng minh tứ giác BFEC nội tiếp được một đường tròn. b) Kẻ đường kính AD của đường tròn (O). Tứ giác BFCD là hình gì? Vì sao? c) Gọi M là trung điểm của BC. Chứng minh AH = 2OM. d) Chứng minh OA | EF
Cho tam giác ABC nhọn có hai đường cao BE, CF nội tiếp đường tròn (O) đường kính AM. Gọi H là trực tâm, K đối xứng với H qua BC. Gọi I là trung điểm của BC.
a) Chứng minh tứ giác AEHF nội tiếp được;
b) Tứ giác BHCM là hình gì?
c) Chứng minh OI = 1/2 AH ;
d) Chứng minh K thuộc đường tròn (O);
e) Chứng minh tứ giác BKMC là hình thang cân
Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O). Kẻ AD là đường kính của (O), AH vuông góc với BC tại H, BE vuông góc với AD tại E. Gọi G là giao điểm của AH với (O).a) Chứng minh tứ giác ABHE nội tiếp và GD ∥ BC;b) Gọi N là giao điểm giữa HE và AC. Chứng minh tam giác AHN vuông tại N;c) Tia phân giác của góc BAC cắt đường tròn (O) tại F. Gọi M là giao điểm của OF và BC, K là trung điểm của AB, I là giao điểm của KM và HE. Chứng minh rằng AB·EI AE·EM.
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Kẻ AD là đường kính của (O), AH vuông góc với BC tại H, BE vuông góc với AD tại E. Gọi G là giao điểm của AH với (O).
a) Chứng minh tứ giác ABHE nội tiếp và GD ∥ BC;
b) Gọi N là giao điểm giữa HE và AC. Chứng minh tam giác AHN vuông tại N;
c) Tia phân giác của góc BAC cắt đường tròn (O) tại F. Gọi M là giao điểm của OF và BC, K là trung điểm của AB, I là giao điểm của KM và HE. Chứng minh rằng AB·EI = AE·EM.