Question

Cho tam giác ABC có ba góc nhọn, biết   A B   =   15 c m ,   A C   =   13 c m và đường cao A H   =   12 c m . Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.

a) Chứng minh rằng ΔAHN ∼ ΔACH

b) Tính độ dài BC

c) Chứng minh ΔAMN ∼ ΔACB

d) Tính MN

Answer 1

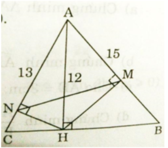
a) Xét ΔANH và ΔAHC có:

∠(NAH) chung

∠(ANH) = ∠(AHN) = 90o

⇒ ΔANH ∼ ΔAHC (g.g)

b) Ta có :

Tương tự : CH = 5 (cm)

⇒ BC = BH + CH = 9 + 5 = 14 (cm)

c) Theo chứng minh trên ta có:

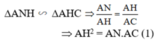
Chứng minh tương tự ta có :

ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)

Từ (1) và (2) ⇒ AN.AC = AM.AB (3)

Xét ΔAMN và ΔACB có :

∠A chung

AN.AC = AM.AB

⇒ ΔAMN ∼ ΔACB (c.g.c)

d) Ta có : ΔAMH ∼ ΔAHB

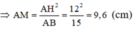
Lại có ΔAMN ∼ ΔACB (cmt)