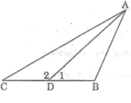
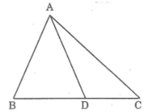
Trong ∆ABD ta có: ∠B > 90o
⇒ ∠B > ∠D1 ( trong 1 tam giác, góc tù là góc lớn nhất- chú ý tổng ba góc trong một tam giác bằng 180º) ⇒ AD > AB (đối diện góc lớn hơn là cạnh lớn hơn) (1)
Trong ΔABD ta có: ∠D2 là góc ngoài tại đỉnh D nên ∠D2 = ∠B + ∠BAD. Suy ra: ∠D2 > ∠B > 90o
Trong ΔADC ta có: ∠D2 > 90o
⇒ ∠D2 > ∠C ⇒ AC > AD (cạnh đối diện góc lớn hơn là cạnh lớn hơn) (2)
Từ (1) và (2) suy ra: AB < AD < AC