Bài1:Cho tam giác ABC,M là điểm nằm trong tam giác. Gọi D là giao điểm của AM và BC, E là giao điểm của BM và CA. F là giao điểm của CM và AB, đường thẳng đi qua M và song song với BC cắt DE, DF lần lượt tại K và I. Cmr MIMK.Bài 2:Cho tam giác ABC, các đường trung tuyến BM, CN cắt nhau tại G, K là điểm trên cạnh BC, đường thẳng đi qua K và song song CN cắt AB ở D, đường thẳng đi qua K và song song với BM cắt AC ở E. Gọi I là giao điểm của KG và DE. Cmr I là trung điểm của DE.Bài 3:Cho tam giác A...
Đọc tiếp
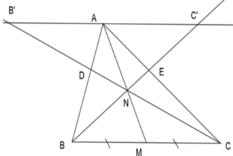
Bài1:Cho tam giác ABC,M là điểm nằm trong tam giác. Gọi D là giao điểm của AM và BC, E là giao điểm của BM và CA. F là giao điểm của CM và AB, đường thẳng đi qua M và song song với BC cắt DE, DF lần lượt tại K và I. Cmr MI=MK.
Bài 2:Cho tam giác ABC, các đường trung tuyến BM, CN cắt nhau tại G, K là điểm trên cạnh BC, đường thẳng đi qua K và song song CN cắt AB ở D, đường thẳng đi qua K và song song với BM cắt AC ở E. Gọi I là giao điểm của KG và DE. Cmr I là trung điểm của DE.
Bài 3:Cho tam giác ABC đều. Gọi M, N là các điểm trên AB, BC sao cho BM=BN. Gọi G là trọng tâm của tam giác BMN. I là trung điểm của AN, P là trung điểm của MN.Cmr:
a, tam giác GPI và tam giác GNC đồng dạng.
b, IC vuông góc với GI.
Bài 4:Cho tam giác ABC vuông tại A, đường cao AH. I là trung điểm của AC, F là hình chiếu của I trên BC. Trên nửa mặt phẳng bờ là đường thẳng chứa AC, vẽ Cx vuông góc với AC cắt IF tại E. Gọi giao điểm của AH, AE với BI theo thứ tự G và K. Cmr:
a,Tam giác IHE và tam giác BHA đồng dạng.
b, Tam giác BHI và tam giác AHE đồng dạng.
c, AE vuông góc với BI.
LÀM ƠN HÃY GIÚP MÌNH NHA. MÌNH ĐANG RẤT VỘI. THANK KIU CÁC BẠN!!!😘😘😘