Áp dụng bất đẳng thức tam giác vào ΔABC , ta có: BC > AB - AC mà AC = AD (gt)
suy ra : BC > AB – AD hay : BC > BD
Vì trong một đường tròn ,dây cung lớn hơn gần tâm hơn nên: OH < OK

Áp dụng bất đẳng thức tam giác vào ΔABC , ta có: BC > AB - AC mà AC = AD (gt)
suy ra : BC > AB – AD hay : BC > BD
Vì trong một đường tròn ,dây cung lớn hơn gần tâm hơn nên: OH < OK
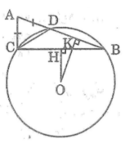
Cho tam giác ABC có AB > AC .Trên cạnh AB lấy điểm D sao cho AD = AC đường tròn tâm O ngoại tiếp tam giác BCD .Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC và BD (H ∈ BC , K ∈ BD). So sánh hai cung nhỏ BD và BC
Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)
Chứng minh rằng OH > OK.
Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)
a) Chứng minh rằng OH > OK.
b) So sánh hai cung nhỏ BD và BC.
Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)
So sánh hai cung nhỏ BD và BC
cho tam giác ABC có AB>AC.trên cạnh AB lấy điểm D sao cho AD=AC.vẽ đường tròn ngoại tiếp tam giác DBC có tâm O.từ O kẻ các đường vuông góc với OH,OK theo thứ tự xuống BC và BD (H thuộc BC,K thuộc BD)
a)cm:OH<OK
b)so sanh hai cung nhỏ BD và BC
Cho \(\Delta ABC\)có AB>AC. Trên cạnh AB lâý một điểm D sao cho AD=AC. Vẽ (O) ngoại tuyến \(\Delta DBC\)Từ O lần lượt hạ các đường vuông góc OH,OK xuống BC, BO ( \(H\in BC,KE\in BD\))
So Sánh a) OH và OK
b) Cung nhỏ BD và BC
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R, đường kính BC với AB < AC
a) tính góc BAC
b) Vẽ đường tròn tâm I, đường kính AO cắt AB, AC lần lượt tại H và K. Chứng minh H, I, K thẳng hàng
c) Tia OH, OK cắt tiếp tuyến tại A với đường tròn tâm O lần lượt tại D, E. Chứng minh BD + CE = DE
d) Chứng tỏ đường tròn đi qua 3 điểm D, O, E tiếp xúc với BC
Cho tam giác ABC nội tiếp đường tròn (O) đường kính BC với AB< AC
a. Tính góc BAC.
b.Vẽ đường tròn (I) đường kính AO cắt AB,AC lần lượt tại H,K. Chứng minh: Ba điểm H,I,K thẳng hàng.
c) Tia OH,OK cắt tiếp tuyến A với (O) lần lượt tại D,E. Chứng minh: BD+CE=DE.
Cho tam giác ABC nội tiếp đường tròn (O;R) đường kính BC với AB<AC
a, tính góc BAC
b,vẽ đường tròn (I) đường kính OA cắt AB , AC lần lượt tại H,K .Chứng minh ba điểm H,I,K thẳng hàng
c, Tia OH, OK cắt tiếp tuyến tại A với (O) lần lượt tại D,E . Chứng minh BD+CE=DE
d,Chứng minh : đường tròn đó qua ba điểm D,O,E tiếp xúc với BC