Question

Cho tam giác ABC có AB = AC = 10cm, BC =12cm. Kẻ AH vuông góc với BC (H thuộc BC)

a) Chứng minh: HB = HC và góc BAH= góc CAH

b) Tính độ dài AH ?

Có vẽ hình

Answer 1

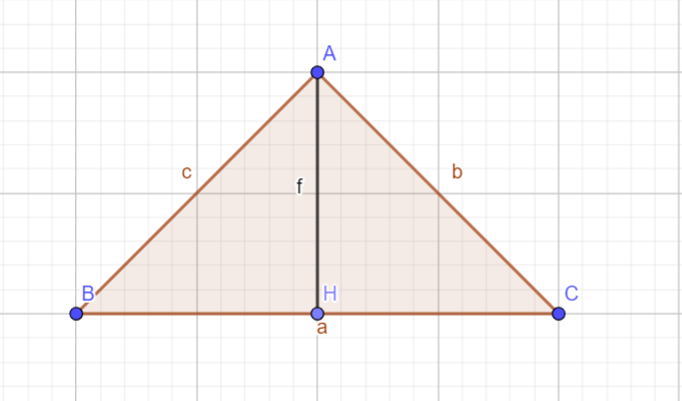
a) Xét tam giác AHB và AHC có:

AC = BC (gt)

\(\widehat{AHB}=\widehat{AHC}\) (AH vuông góc BC)

=> AHB = AHC (ch-gv)

=> HB = HC (cạnh tương ứng)

\(\widehat{BAH}=\widehat{CAH}\) (góc tương ứng)

b) Ta có HB =  HC (cmt)

Mặt khác AH là cạnh góc vuông của tam giác vuông AHC

Áp dụng định lý Pitago ta có:

\(AC^2=AH^2+HC^2\\ =>10^2=AH^2+6^2\\ =>100=AH^2+36\)

\(=>AH^2=100-36=64\\ =>AH=\sqrt{64}=8\)