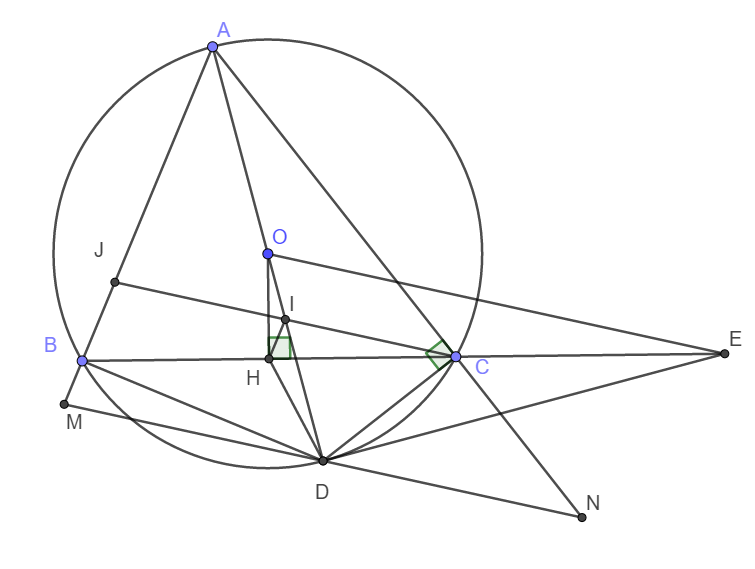
Cho tam giác ABC có 3 góc nhọn (AB<AC) nội tiếp đường tròn (O;R). Vẽ đường kính AD, tiếp tuyến với đường tròn (O;R) tại D cắt BC tại E. Vẽ OH vuông góc với BC
a/ Chứng minh tứ giác OHDE nội tiếp
b/ Chứng minh ED^2=EC.EB
c/ Từ C vẽ đường thẳng song song với EO cắt AD tại I. Chứng minh HI song song với AB
d/ Qua D vẽ đường thẳng song song với EO cắt AB và AC lần lượt tại M nà N. Chứng minh DM=DN
a) Ta có: DE là tiếp tuyến của (O) nên ^ODE=900 . Mà OH vuông góc BE
=> ^OHE=900 => ^ODE=^OHE.
Xét tứ giác OHDE: ^OHE=^ODE=900 => Tứ giác OHDE nội tiếp đường tròn. (đpcm).
b) Dễ thấy ^EDC=^EBD (T/c góc tạo bởi tiếp tuyến và dây cung)
=> \(\Delta\)ECD ~ \(\Delta\)EDB (g.g) => \(\frac{ED}{EB}=\frac{EC}{ED}\Rightarrow ED^2=EC.EB.\)(đpcm).
c) Tứ giác OHDE nội tiếp đường tròn (cmt) => ^OEH=^ODH.
Lại có: CI//OE => ^OEH=^ICH => ^ICH=^ODH hay ^ICH=^IDH
=> Tứ giác HICD nội tiếp đường tròn => ^HID=^HCD=^BCD
Do tứ giác ABDC nội tiếp (O) => ^BCD=^BAD.
Do đó ^HID=^BAD. Mà 2 góc bên ở vị trí đồng vị => HI//AB (đpcm).
d) Gọi giao điểm của tia CI với AB là P.
Ta thấy: Đường tròn (O) có dây cung BC và OH vuông góc BC tại H => H là trung điểm BC.
Xét \(\Delta\)BPC: H là trung điểm BC; HI//BP (HI//AB); I thuộc CP => I là trung điểm CP => IC=IP (1)
Theo hệ quả của ĐL Thales; ta có: \(\frac{IP}{DM}=\frac{AI}{AD};\frac{IC}{DN}=\frac{AD}{AI}\Rightarrow\frac{IP}{DM}=\frac{IC}{DN}\)(2)
Từ (1) và (2) => DM=DN (đpcm).
Chỗ \(\frac{IC}{DN}=\frac{AD}{AI}\)bạn sửa thành \(\frac{IC}{DN}=\frac{AI}{AD}\)nha.
a) Do DE là tiếp tuyến của đường tròn (O) tại D nên \(OD\perp DE\Rightarrow\widehat{ODE}=90^o\)
Xét tứ giác OHDE có: \(\widehat{OHE}=\widehat{ODE}=90^o\) mà H, D là hai đỉnh kề nhau nên OHDE là tứ giác nội tiếp (Dấu hiệu)
b) Xét tam giác EDC và tam giác EBD có:
Góc E chung
\(\widehat{CDE}=\widehat{DBE}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung DC)
\(\Rightarrow\Delta EDC\sim\Delta EBD\left(g-g\right)\)
\(\Rightarrow\frac{ED}{EB}=\frac{EC}{ED}\Rightarrow ED^2=EC.EB\)
c) Do tứ giác OHDE nội tiếp nên \(\widehat{OEH}=\widehat{ODH}\) (Hai góc nội tiếp cùng chắn cung OH)
Lại do IC // OE nên \(\widehat{OEH}=\widehat{ICH}\) (Hai góc đồng vị)
Vậy nên \(\widehat{ICH}=\widehat{IDH}\)
Suy ra tứ giác IHDC là tứ giác nội tiếp.
Từ đó ta có: \(\widehat{HID}=\widehat{HCD}\) (Hai góc nội tiếp cùng chắn cung DH)
Lại có tứ giác ABDC cũng nội tiếp nên \(\widehat{HCD}=\widehat{BAD}\)(Hai góc nội tiếp cùng chắn cung DB)
Vậy nên \(\widehat{HID}=\widehat{BAD}\). Chúng lại ở vị trí đồng vị nên HI // AB.
d) Gọi J là giao điểm của CI và AB.
Do OH vuông góc BC nên theo tính chất đường kính dây cung thì H là trung điểm BC.
Xét tam giác BCJ có H là trung điểm BC, HI // BJ nên HI là đường trung bình tam giác BCJ.
Suy ra I là trung điểm CJ.
Ta có CJ // OE, MN // OE nên CJ// MN.
Áp dụng hệ quả định lý Talet ta có:
\(\frac{IJ}{MD}=\frac{AI}{AD}=\frac{IC}{DN}\)
Do IJ = IC nên MD = DN (đpcm)

