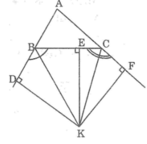
Gọi K là giao điểm của hai tia phân giác của góc ngoài tại đỉnh B và góc ngoài tại đỉnh C.
Kẻ KE ⊥ BC, KF ⊥ AC, KD ⊥ AB
Vì K nằm trên phân giác của ∠(CBD) nên:
KD = KE (tính chất tia phân giác) (1)
Vì K nằm trên tia phân giác của ∠(BCF) nên:
KE = KF (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: KD = KF
Điểm K nằm trong ∠(BAC) cách đều 2 cạnh AB và AC nên K nằm trên tia phân giác của ∠(BAC) .