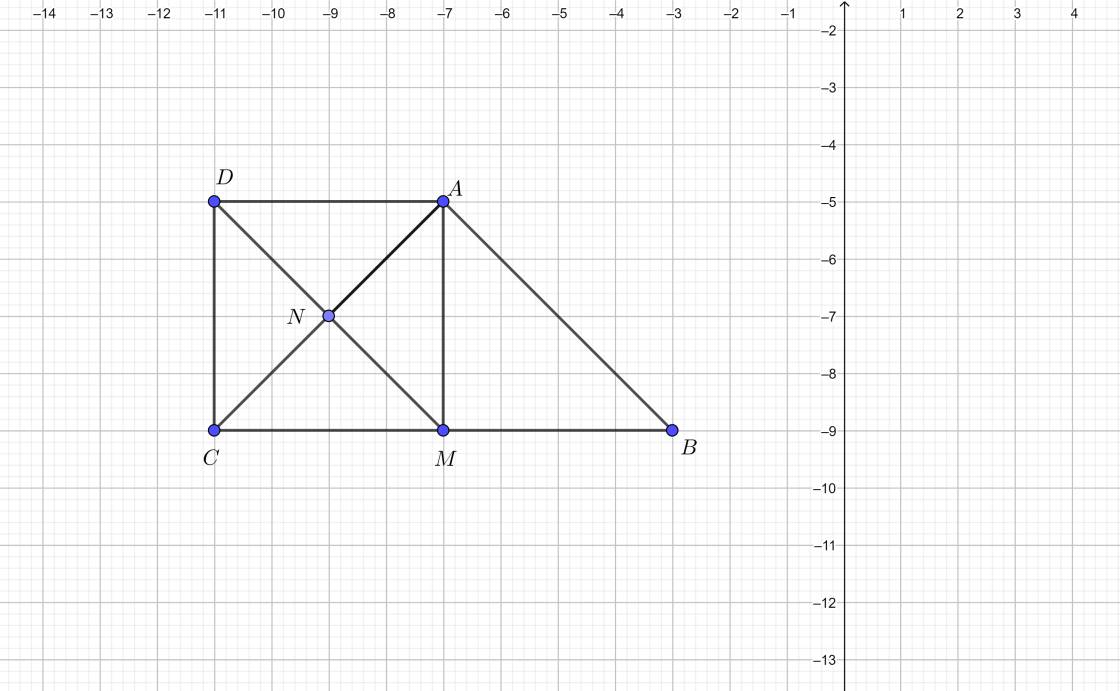
a)vì N là trung điểm AC nên AN=NC
D đối xứng với M qua N nên MN=MD
suy ra tứ giác AMCD là HBH
mà ABC cân tại A nên trung tuyến AH cũng là đường cao(AH⊥BC)
do đó HBH AMCD là HCN
b)vì N là trung điểm AC nên MN là đường trung tuyến trong △ vuông AMC
=>MN=1/2AC=>AC=2MN=2.6=12cm
c)vì Tứ giác AMCD là HCN nên MD=AC
mà AC=AB(△ABC cân tại A)=>MD=AB (1)
và DA//CM =>DA//BC (2)
từ (1) và (2) =>tứ giác ABMD là HBH
=>MD//AB
` a)D ` là điểm đối xứng với ` M ` qua điểm ` N `
` =>N ` là trung điểm ` DM `
Tứ giác ` AMCD ` có giao điểm của hai đường chéo ` AC ` và ` DM ` là trung điểm của mỗi đường tức điểm ` N `
` => AMCD ` là hình bình hành
Tam giác ` ABC ` cân tại ` A ` có ` AM ` là đường trung tuyến đồng thời là đường cao
` =>\hat{M}=90^o ` có ` AMCD ` là hình bình hành
` =>\hat{D}=\hat{M}=90^o( ` Tính chất hình bình hành ` ) `
` AMCD ` là hình bình hành ` =>CD////AM `
` =>\hat{D}+\hat{A}=180^o( ` Hai góc trong cùng phía bù nhau ` ) `
` =>90^o+\hat{A}=180^o=>\hat{A}=90^o `
` =>AMCD ` là hình chữ nhật
` b) ` Tam giác ` ACM ` vuông tại ` M ` có ` MN ` là đường trung tuyến
` =>MN=1/2 AC=>AC=2MN=2.6=12(cm) `
` c)AMCD ` là hình chữ nhật ` =>AD////CM ` và ` AD=CM `
Mà ` M ` là trung điểm ` BC(M ` thuộc cạnh ` BC) `
` =>AD////MB ` và ` AD=MB=> ` Tứ giác ` ADMB ` có một cặp cạnh song song và bằng nhau
` =>ADMB ` là hình bình hành
` =>MD////AB `