Các câu hỏi tương tự
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.
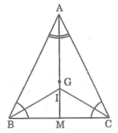
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường thẳng phân giác. Chứng minh rằng ba điểm A,G,I thẳng hàng
cho tam giác ABC cân tại A . Gọi G là trọng tâm của tam giác , gọi I là giao điểm các đường phân giác của tam giác . Chứng minh rằng ba điểm A,G,I thẳng hàng.
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.
cho tam giác ABC cân tại A . gọi G là trọng tâm của tam giác . I là giao điểm các phân giác của tam giác . chứng minh: ba điểm A, G,I thẳng hàng
Cho tam giác nhọn ABC ( tam giác thường). Họi H,G,O theo thứ tự là trực tâm, trọng tâm, giao điểm ba đường trung trực của tam giác. Tia AG cắt BC ở M. Gọi I là trung điểm của GH. Chứng minh:
a) OM = 1/2 AH
b) tam giác IGK = tam giác MGO
c) Ba điểm H,O,G thẳng hàng
d) GH=2GO
cho tam giác ABC cân tại A. Gọi G là trọng tâm tam giác, I là giao điểm các phân giác của tam giác. Chứng minh: 3 điểm A,G,I thẳng hàng
cho tam giác abc /cân tại a đường cao ah đường thẳng qua h song song với ab cắt ac tại k . bk cắt ah tại g . gọi i là trung điểm của ab cmr
a/ G là trọng tâm tam giác abc
b/ Ba điểm i,g,c thẳng hàng
c/ KI là đường trung trực của ah
giúp mik với
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.

