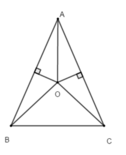
+ Vì O thuộc đường trung trực của AB nên OA = OB, do đó đáp án A sai
+ Vì ba đường trung trực của tam giác đồng quy tại một điểm nên O là giao điểm của ba đường trung trực của tam giác ABC, suy ra O thuộc đường trung trực cạnh BC
Mà AB = AC nên A thuộc đường trung trực cạnh BC
Do đó AO là đường trung trực của BC ⇒ A O ⊥ B C , nên đáp án C đúng
+ Lại có tam giác ABC cân tại A (AB = AC) có AO là trung trực nên AO cũng là phân giác của góc BAC ⇒ B A O ^ = C A O ^
Khi đó Δ B A O = Δ C A O ( c – g – c) (vì AB = AC, AO chung, B A O ^ = C A O ^ )
Suy ra A O B ^ = A O C ^ ⇒ Đáp án B sai
+ Do tam giác ABC là tam giác cân không đều nên O không phải là giao điểm của ba đường phân giác trong tam giác ABC nên O không cách đều ba cạnh của tam giác ABC, do đó đáp án D sai.
Chọn đáp án C

