Question

Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:

Bốn điểm B, E, D, C cùng thuộc một đường tròn.

Answer 1

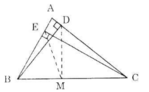
Gọi M là trung điểm của BC.

=> ME = MB = MC = MD

Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)

Answer 2

a) Gọi O là trung điểm của BC ( OB = OC )

+) Xét tam giác vuông EBC ( ^BEC = 90^o )

EO là đường trung tuyến

\(\Rightarrow EO=\frac{1}{2}BC\)

\(\Rightarrow OE=OB=OC\left(1\right)\)

+) Xét tam giác vuông DBC ( ^CDB = 90^o )

DO là đường trung tuyến \(\Rightarrow DO=\frac{1}{2}BC\)

=> DO = OB = OC (2)

Từ (1)(2) => OD = OE = OB = OC

Vậy : 4 điểm B , E , D , C cùng thuộc đường tròn đường trình BC ( đpcm )