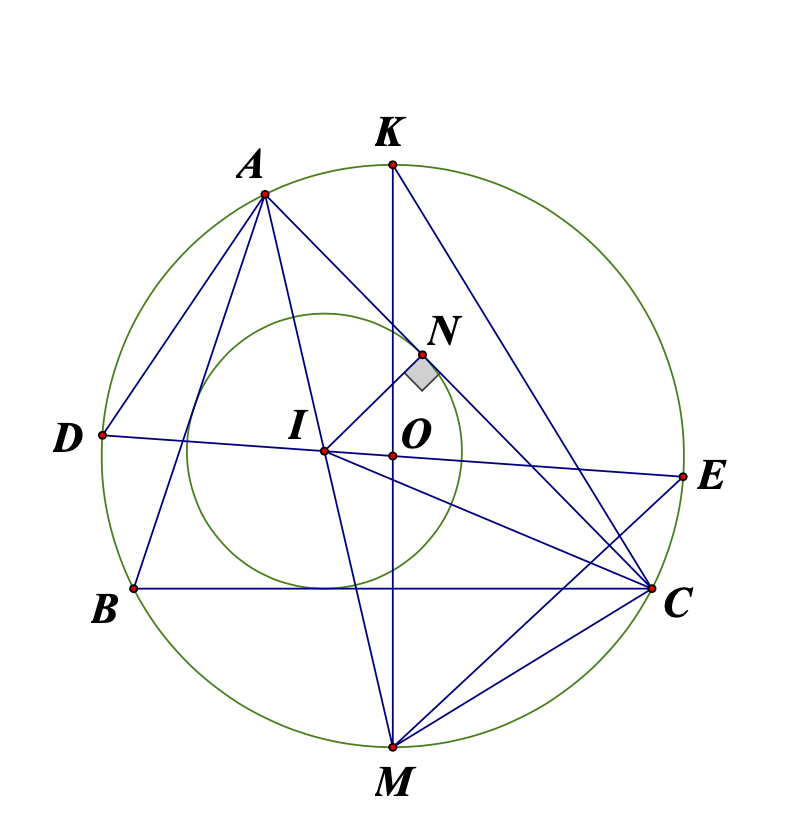
Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O) có AD, BE là hai đường cao cắt nhau tại H, vẽ đường kính AK của đường tròn (O), kẻ BF⊥AK (F∈AK).
a) Chúng minh 5 điểm A,B,C,D,E,F cùng thuộc một đường tròn, xác định tâm I của đường tròn này.
b) Gọi M là trung điểm của BC. Chứng 3 điểm H,M,K thẳng hàng.
c)Chứng minh IM là đường trung trực của DF
a) Sửa đề: 5 điểm A,B,D,F,E cùng thuộc một đường tròn
Xét tứ giác ABFE có
\(\widehat{AFB}=\widehat{AEB}\left(=90^0\right)\)
\(\widehat{AFB}\) và \(\widehat{AEB}\) là hai góc cùng nhìn cạnh AB
Do đó: ABFE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: A,B,F,E cùng thuộc 1 đường tròn(1)
Xét tứ giác ABDE có
\(\widehat{ADB}=\widehat{AEB}\left(=90^0\right)\)
\(\widehat{ADB}\) và \(\widehat{AEB}\) là hai góc cùng nhìn cạnh AB
Do đó: ABDE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: A,B,D,E cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,B,D,F,E cùng thuộc 1 đường tròn(đpcm)
Tâm I của đường tròn này là trung điểm của AB