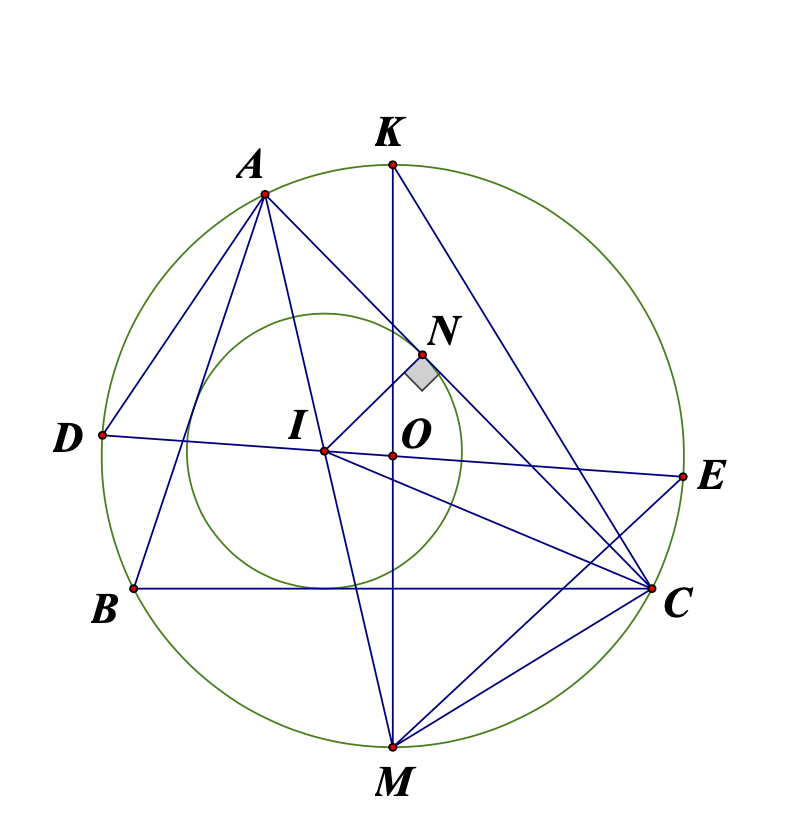
xét tứ giác BPNC:
\(\widehat{P}=90\) (CP là đường cao)
\(\widehat{N}\)=90 (BN là đường cao)
⇒ \(\widehat{P}=\widehat{N}\)= 180
⇒ tứ giác BPNC là tứ giác nội tiếp
xét tứ giác A'SNC:
\(\widehat{N}=90\) (BN là đường cao)
\(\widehat{S}=90\) (PN\(\perp\)AB ⇒ NS\(\perp\)AB)
⇒\(\widehat{N}=\widehat{S}=180\)
⇒ tứ giác A'SNC là tứ giác nội tiếp