Đáp án B.
Phương pháp giải: Số phức z=a+bi có môđun là z = a 2 + b 2
Lời giải: Ta có
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho số phức z thỏa mãn |z + 3| = 5 và |z - 2i| = |z - 2 - 2i|. Tính |z|
A. |z| = 17
B. |z| = 17
C. |z| = 10
D. |z| = 10
Tìm số phức z thỏa mãn
z
¯
1
3
(
1
-
2
i
)
¯
2
-
z
. ...
Đọc tiếp
Tìm số phức z thỏa mãn z ¯ = 1 3 ( 1 - 2 i ) ¯ 2 - z .
A. - 3 4 - 2i
B. - 3 4 + 2i
C. 2 + 3 4 i
D. 2 - 3 4 i
Tìm số phức z thỏa mãn
z
¯
1
3
(
1
-
2
i
)
¯
2
-
z
....
Đọc tiếp
Tìm số phức z thỏa mãn z ¯ = 1 3 ( 1 - 2 i ) ¯ 2 - z .
A . - 3 4 - 2 i
B . - 3 4 + 2 i
C . 2 + 3 4 i
D . 2 - 3 4 i
Cho số phức z thỏa mãn
z
2
-
2
z
+
5
(
z
-
1
+
2
i
)
(
z
+
3
i
-...
Đọc tiếp
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính m i n w , với w = z - 2 + 2 i .
A. m i n w = 3 2
B. m i n w = 2
C. m i n w = 1
D. m i n w = 1 2
Cho số phức z thỏa mãn
z
2
-
2
z
+
5
(
z
-
1
+
2
i
)
(
z
+...
Đọc tiếp
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính min |w|, với w = z - 2 + 2 i
Cho số phức z a + bi (a,b
∈
ℝ
) thỏa mãn z + 2i
z
¯
3 + 3i. Tính z. A. |z| 2 B. |z|
5
C. |z| 5 D. |z|
2
Đọc tiếp
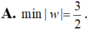
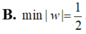
Cho số phức z = a + bi (a,b ∈ ℝ ) thỏa mãn z + 2i z ¯ = 3 + 3i. Tính z.
A. |z| = 2
B. |z| = 5
C. |z| = 5
D. |z| = 2
Có bao nhiêu số phức z thỏa mãn
(
1
+
i
)
z
+
(
2
-
i
)
z
¯
13
+
2
i
? A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn ( 1 + i ) z + ( 2 - i ) z ¯ = 13 + 2 i ?
A. 4
B. 3
C. 2
D. 1
Có bao nhiêu số phức z thỏa mãn
(
1
+
i
)
z
+
(
2
-
i
)
z
¯
13
+
2
i
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn ( 1 + i ) z + ( 2 - i ) z ¯ = 13 + 2 i
Cho số phức z thỏa điều kiện
z
+
2
z
+
2
i
. Giá trị nhỏ nhất của biểu thức
P
z
-
1
-
2...
Đọc tiếp
Cho số phức z thỏa điều kiện z + 2 = z + 2 i . Giá trị nhỏ nhất của biểu thức P = z - 1 - 2 i + z - 3 - 4 i + z - 5 - 6 i được viết dưới dạng a + b 17 2 với a, b là các hữu tỉ. Giá trị của a + b là
A. 4.
B. 2.
C. 7.
D. 3.
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) 5
z
¯
. Tìm phần ảo của số phức w
(
z
+
2
i
)
2019
A
.
2
1009
B
.
0
C
.
-
2...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5 z ¯ . Tìm phần ảo của số phức w = ( z + 2 i ) 2019
A . 2 1009
B . 0
C . - 2 1009
D . 2019